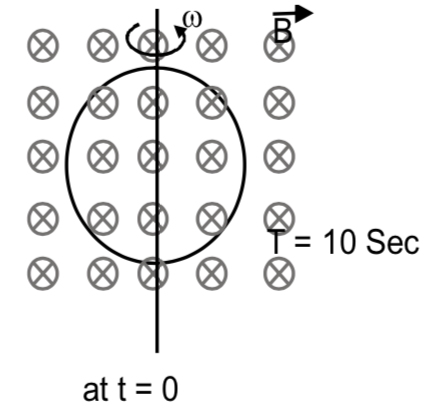
A ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
2.5 s and 5.0 s
5.0 s and 7.5 s
2.5 s and 7.5 s
5.0 s and 10.0 s
The correct Answer is:2
To solve the problem, we need to determine the instances of time at which the induced electromotive force (EMF) in a rotating ring is at its maximum and minimum. The ring is rotating about a diametric axis in a uniform magnetic field that is perpendicular to the plane of the ring.
1. Understand the Setup:
- The ring is initially perpendicular to the magnetic field.
- As it rotates, the angle between the area vector of the ring and the magnetic field changes.
2. Define the Variables:
- Let B be the magnetic field strength.
- Let A be the area of the ring.
- The angular velocity ω can be defined as ω=2πT, where T is the time period of rotation.
3. Calculate the Induced EMF:
- The magnetic flux Φ through the ring at any time t can be expressed as:
Φ=B⋅A⋅cos(θ)
- Here, θ=ωt is the angle between the magnetic field and the area vector of the ring.
- Therefore, the flux becomes:
Φ=B⋅A⋅cos(ωt)
- The induced EMF E is given by Faraday's law:
E=−dΦdt=−ddt(B⋅A⋅cos(ωt))
- This leads to:
E=B⋅A⋅ω⋅sin(ωt)
4. Determine Maximum EMF:
- The EMF will be maximum when sin(ωt)=1.
- This occurs at:
ωt=π2
- Substituting ω=2πT:
2πTt=π2
- Solving for t:
t=T4
- Given T=10 seconds, we find:
tmax=104=2.5 seconds
5. Determine Minimum EMF:
- The EMF will be minimum when sin(ωt)=0.
- This occurs at:
ωt=nπ(n=0,1,2,…)
- The first minimum occurs at n=1:
2πTt=π
- Solving for t:
t=T2
- Given T=10 seconds, we find:
tmin=102=5 seconds
Final Answer:
- The instant of time at which the EMF will be maximum is 2.5 seconds.
- The instant of time at which the EMF will be minimum is 5 seconds.
- The ring is initially perpendicular to the magnetic field.
- As it rotates, the angle between the area vector of the ring and the magnetic field changes.
- Let B be the magnetic field strength.
- Let A be the area of the ring.
- The angular velocity ω can be defined as ω=2πT, where T is the time period of rotation.
- The magnetic flux Φ through the ring at any time t can be expressed as:
Φ=B⋅A⋅cos(θ)
- Here, θ=ωt is the angle between the magnetic field and the area vector of the ring.
- Therefore, the flux becomes:
Φ=B⋅A⋅cos(ωt)
- The induced EMF E is given by Faraday's law:
E=−dΦdt=−ddt(B⋅A⋅cos(ωt))
- This leads to:
E=B⋅A⋅ω⋅sin(ωt)
- The EMF will be maximum when sin(ωt)=1.
- This occurs at:
ωt=π2
- Substituting ω=2πT:
2πTt=π2
- Solving for t:
t=T4
- Given T=10 seconds, we find:
tmax=104=2.5 seconds
- The EMF will be minimum when sin(ωt)=0.
- This occurs at:
ωt=nπ(n=0,1,2,…)
- The first minimum occurs at n=1:
2πTt=π
- Solving for t:
t=T2
- Given T=10 seconds, we find:
tmin=102=5 seconds
- The instant of time at which the EMF will be maximum is 2.5 seconds.
- The instant of time at which the EMF will be minimum is 5 seconds.
Topper's Solved these Questions
Similar Questions
A ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
 )
)
View Solutionthe uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
the uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View SolutionA circular conducting ring is rotated about one of its diameter in a magnetic field
View SolutionA rectangular coil of area A rotates in a uniform magnetic field B with angular velocity about an axis perpendicular to the field, initially the plane of coil is perpendicular to the field,then the avarage induced e.m.f. after rotating by 90° is
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View Solution
