Assume x=2cos(πt+π3) cm represents the position of a particle performing SHM. The initial position of particle on x-axis is
2 cm
1 cm
4 cm
3 cm
To find the initial position of the particle on the x-axis, we will evaluate the given equation of motion at time t=0.
1. Write down the equation of motion:
The position of the particle is given by:
x=2cos(πt+π3) cm
2. Substitute t=0:
To find the initial position, we substitute t=0 into the equation:
x=2cos(π⋅0+π3)
3. Simplify the expression:
This simplifies to:
x=2cos(π3)
4. Calculate cos(π3):
We know that:
cos(π3)=12
Therefore, substituting this value back into the equation gives:
x=2⋅12
5. Final calculation:
Simplifying this, we find:
x=1 cm
Thus, the initial position of the particle on the x-axis is 1 cm.
The position of the particle is given by:
x=2cos(πt+π3) cm
To find the initial position, we substitute t=0 into the equation:
x=2cos(π⋅0+π3)
This simplifies to:
x=2cos(π3)
We know that:
cos(π3)=12
Therefore, substituting this value back into the equation gives:
x=2⋅12
Simplifying this, we find:
x=1 cm
Similar Questions
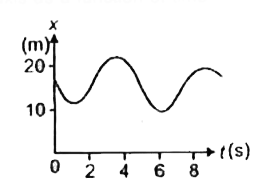
Figure shows the position of a particle moving on the X-axis as a function of time.

View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
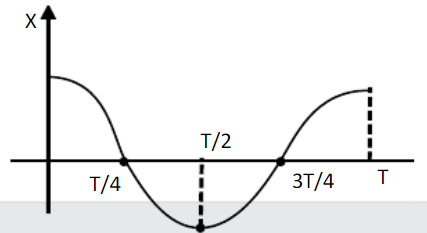
View SolutionDisplacement time graph of particle performing SHM is as shown in figure. Assume that mean position is at x=0
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionAccording to a scientists, he applied a force F=−cx1/3 on a particle and the particle is performing SHM. No other force acted on the particle. He refuses to tell whether c is a constant or not. Assume that he had worked only with positive x then :
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The maximum value of position co-ordinate of particle on positive x-axis is
View SolutionA particle executes linear SHM with amplitude A and mean position is x=0. Determine position of the particle where potential energy of the particle is equal to its kinetic energy.
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
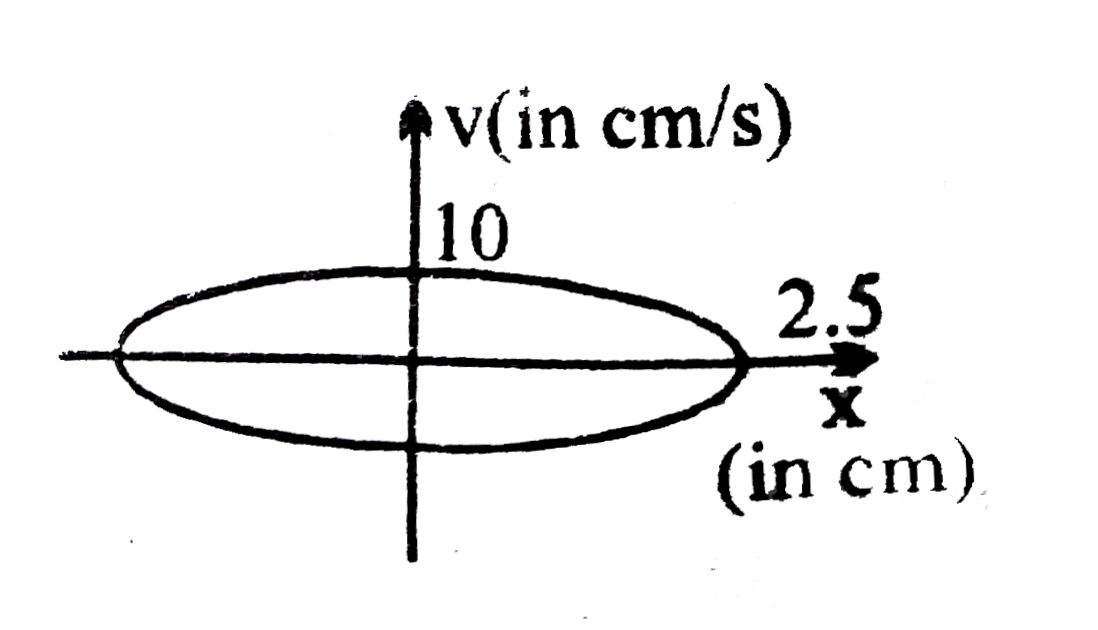
View Solution
