The amplitude of a particle under forced vibration is given as A=10x2−5x+6. Resonance will takes place at x equal to
A. 5/2
B. Zero
C. 2
D. 4
Step by step video & image solution for The amplitude of a particle under forced vibration is given as A=10/(x^2-5x+6). Resonance will takes place at x equal to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
The position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
View SolutionThe rate of doing work by force acting on a particle moving along x-axis depends on position x of particle and is equal to 2x. The velocity of particle is given by expression :-
View SolutionFor a particle showing motion under forces F=−5(x−2)2 , the motion is
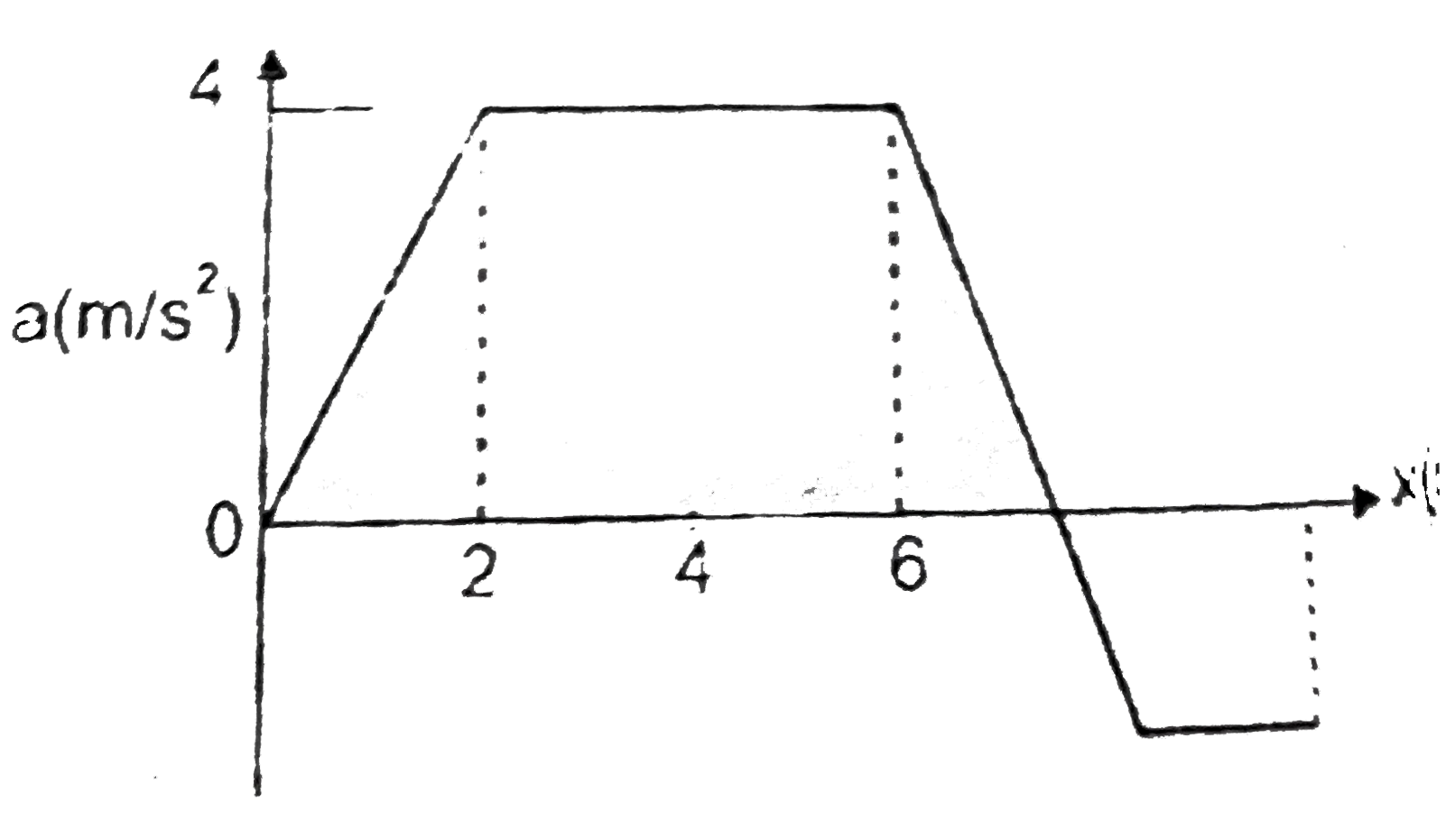
View SolutionGraphs shows the acceleration of a 3 kg particle as an applied force moves it from rest along x-axis. The total work done by the force on the particle by the time the particle reaches x = 6 m, is equal to
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionA particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by −kx2ˆi. If the particle starts from rest at x=a, the speed it will attain when it crosses the origin is
View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction. The amplitude of oscillation is 4×10−3m. The least period of these oscillations, so that the object is not detached from the platform is π5x second. Find value of x. Take g=10m/s2
View Solution
