The rate of doing work by force acting on a particle moving along x-axis depends on position x of particle and is equal to 2x. The velocity of particle is given by expression :-
[3x2m]1/3
[3x22m]1/3
(2mx9)1/2
[mx23]1/2
The correct Answer is:A
To find the velocity of a particle moving along the x-axis where the rate of doing work by the force is given as P=2x, we can follow these steps:
Step 1: Understand the relationship between power, force, and velocity
The rate of doing work (power) is given by the formula:
P=F⋅v
where F is the force acting on the particle and v is its velocity.
Step 2: Set up the equation using the given power
From the problem, we know that:
P=2x
Thus, we can write:
F⋅v=2x
Step 3: Relate force to mass and acceleration
According to Newton's second law, the force can also be expressed as:
F=m⋅a
where m is the mass of the particle and a is its acceleration. We can express acceleration in terms of velocity and position:
a=dvdt=vdvdx
Substituting this into the force equation gives:
F=m⋅vdvdx
Step 4: Substitute force into the power equation
Now we can substitute this expression for force back into the power equation:
m⋅vdvdx⋅v=2x
This simplifies to:
mv2dvdx=2x
Step 5: Rearrange the equation for integration
Rearranging gives:
v2dv=2mxdx
Step 6: Integrate both sides
Now we integrate both sides:
∫v2dv=2m∫xdx
This results in:
v33=2m⋅x22+C
The constant C can be determined based on initial conditions, but for this problem, we can assume C=0 for simplicity.
Step 7: Simplify the equation
This simplifies to:
v33=x2m
Multiplying both sides by 3 gives:
v3=3x2m
Step 8: Solve for velocity
Taking the cube root of both sides, we find:
v=(3x2m)13
Final Answer
Thus, the velocity of the particle is given by:
v=(3m)13x23
---
The rate of doing work (power) is given by the formula:
P=F⋅v
where F is the force acting on the particle and v is its velocity.
From the problem, we know that:
P=2x
Thus, we can write:
F⋅v=2x
According to Newton's second law, the force can also be expressed as:
F=m⋅a
where m is the mass of the particle and a is its acceleration. We can express acceleration in terms of velocity and position:
a=dvdt=vdvdx
Substituting this into the force equation gives:
F=m⋅vdvdx
Now we can substitute this expression for force back into the power equation:
m⋅vdvdx⋅v=2x
This simplifies to:
mv2dvdx=2x
Rearranging gives:
v2dv=2mxdx
Now we integrate both sides:
∫v2dv=2m∫xdx
This results in:
v33=2m⋅x22+C
The constant C can be determined based on initial conditions, but for this problem, we can assume C=0 for simplicity.
This simplifies to:
v33=x2m
Multiplying both sides by 3 gives:
v3=3x2m
Taking the cube root of both sides, we find:
v=(3x2m)13
Thus, the velocity of the particle is given by:
v=(3m)13x23
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - C)
Explore 80 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - D)
Explore 13 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - A)
Explore 64 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
Force acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
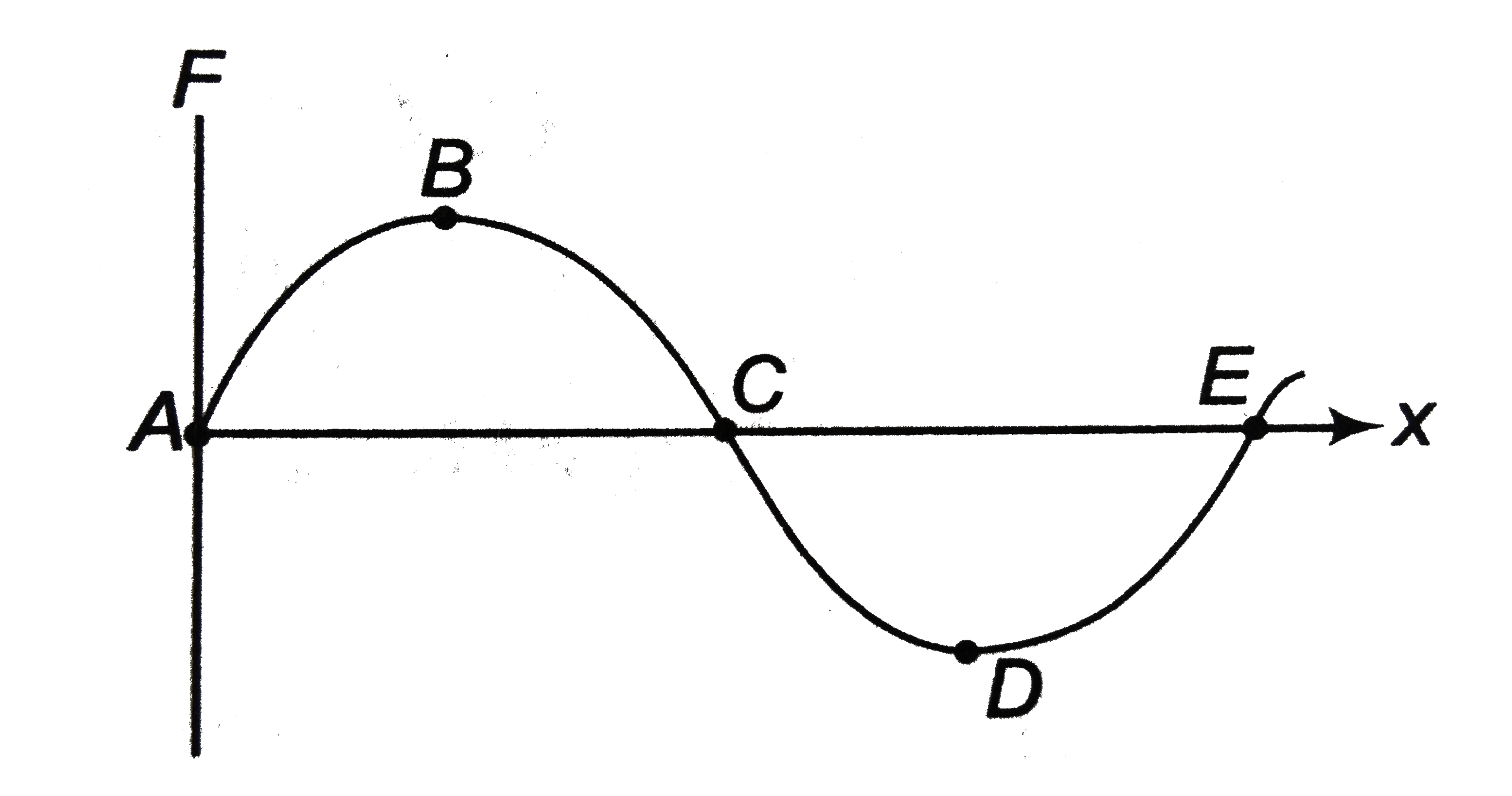 .
.
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be

View Solutionx-t equation of a particle moving along x-axis is given as
x=A+A(1−cosωt)
View SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
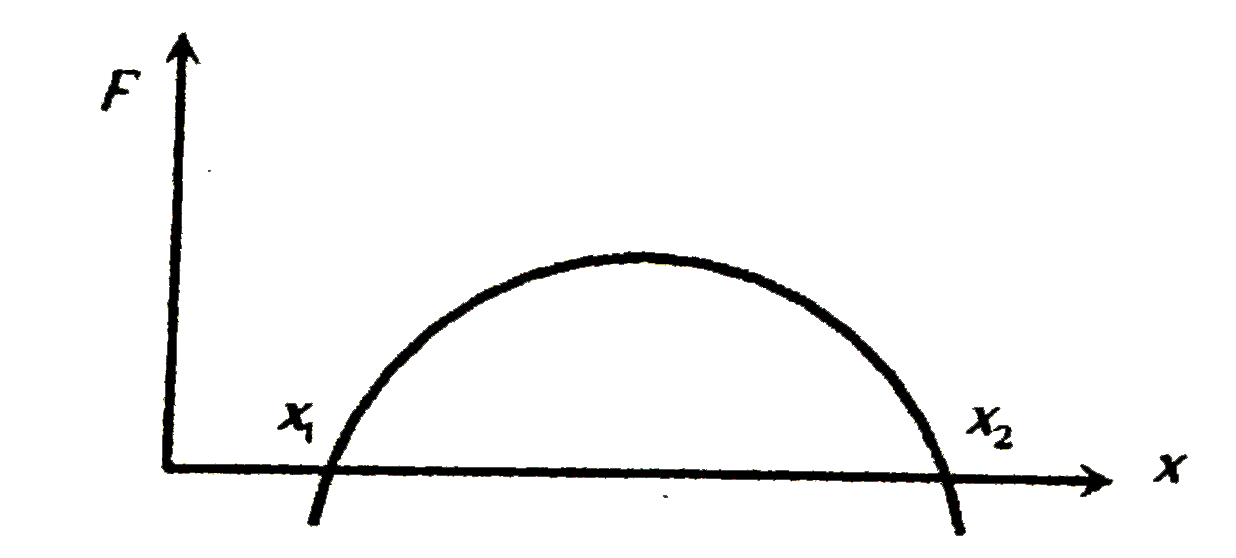
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionThe force acting on a body moving along x-axis variation of the particle particle shown in the figure. The body is in stable equilibrium at
 .
.
View SolutionThe force acting on a body moving along x-axis variation of the particle particle shown in the figure. The body is in stable equilibrium at
 .
.
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
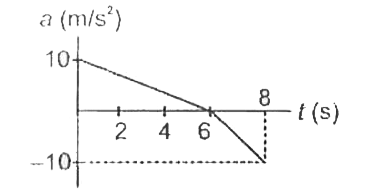
View Solution