Two identical short bar magnets of magnetic moment M each are placed at distance r apart in end-on position, then magnetic force between both is
(μ04π).(M2r2)
(μ04π).(4M2r4)
(μ04π).(6M2r4)
(μ04π).(6M2r2)
To solve the problem of finding the magnetic force between two identical short bar magnets placed at a distance r apart in an end-on position, we can follow these steps:
1. Identify the Given Data:
- Magnetic moment of each magnet, M.
- Distance between the magnets, r.
2. Understand the Formula for Magnetic Force:
- The formula for the magnetic force F between two magnetic dipoles (bar magnets) is given by:
F=μ04π⋅m1m2d4
where:
- μ0 is the permeability of free space,
- m1 and m2 are the magnetic moments of the two magnets,
- d is the distance between the magnets.
3. Substitute the Values:
- Since both magnets are identical, we have m1=M and m2=M.
- Therefore, we can rewrite the formula as:
F=μ04π⋅M⋅Mr4
- This simplifies to:
F=μ04π⋅M2r4
4. Final Expression:
- The final expression for the magnetic force between the two identical short bar magnets is:
F=μ04π⋅M2r4
5. Conclusion:
- Thus, the magnetic force between the two magnets when placed in an end-on position at a distance r apart is:
F=μ04π⋅M2r4
- Magnetic moment of each magnet, M.
- Distance between the magnets, r.
- The formula for the magnetic force F between two magnetic dipoles (bar magnets) is given by:
F=μ04π⋅m1m2d4
where:
- μ0 is the permeability of free space,
- m1 and m2 are the magnetic moments of the two magnets,
- d is the distance between the magnets.
- Since both magnets are identical, we have m1=M and m2=M.
- Therefore, we can rewrite the formula as:
F=μ04π⋅M⋅Mr4
- This simplifies to:
F=μ04π⋅M2r4
- The final expression for the magnetic force between the two identical short bar magnets is:
F=μ04π⋅M2r4
- Thus, the magnetic force between the two magnets when placed in an end-on position at a distance r apart is:
F=μ04π⋅M2r4
Similar Questions
Two identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
View SolutionTwo identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View Solution
Knowledge Check
Two identical magnetic dipoles of magnetic moments 1⋅0Am2 each are placed at a separation of 2m with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
A√5×10−7TB5×10−7TC√2×10−7TD10−7T
Two identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
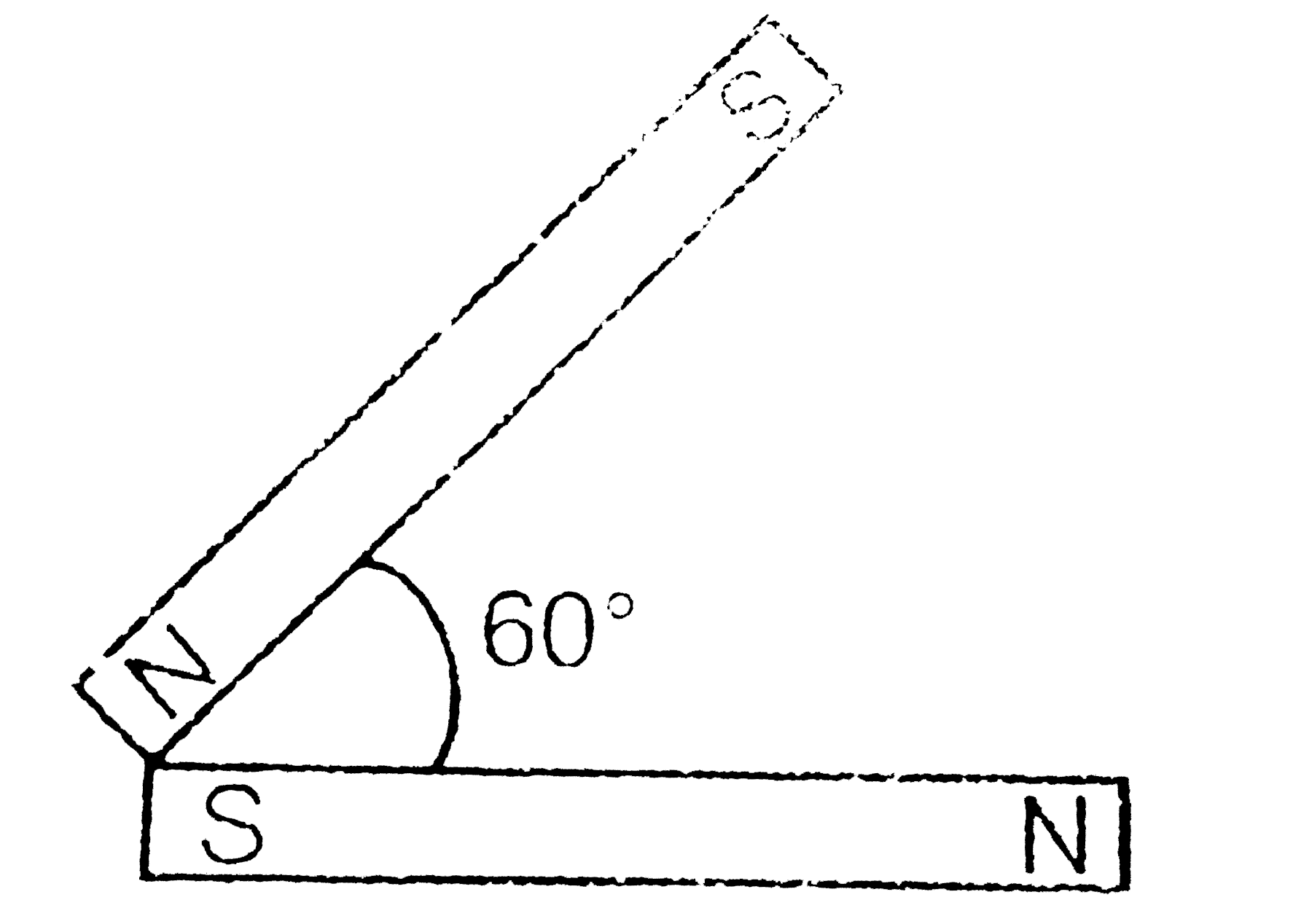
View SolutionA bar magnet of magnetic moment M is cut into four identical parts as shown in figure, then magnetic moment of each part is
_PHY_E06_282_Q01.png)
View SolutionTwo identical magnetic dipoles of magnetic moments 1⋅0Am2 each are placed at a separation of 2m with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
View SolutionFigure shows two identical magnetic dipoles aandb of magnetic moments M each, placed at a separation d, with their axes perpendicular to each other. Find the magnetic field at the point P midway between the dipoles.

View SolutionTwo magnets of equal magnetic moments M each are placed as shown in figure below . The resultant magnetic moment is M . Then value of θ is

View SolutionA bar magnet of magnetic moment →M is placed in a magnetic field of induction →B . The torque exerted on it is
View SolutionA bar magnet of magnetic moment M is bent in the form of quadrant of circular arc . The new magnetic moment is
View Solution