A bar magnet of magnetic moment M is bent in the form of quadrant of circular arc . The new magnetic moment is
2Mπ
2√2Mπ
√2Mπ
M
The correct Answer is:B
To solve the problem of finding the new magnetic moment of a bar magnet bent into the form of a quadrant of a circular arc, we can follow these steps:
1. Understand the Original Magnetic Moment:
The magnetic moment M of a bar magnet is given by the formula:
M=m⋅L
where m is the pole strength and L is the length of the magnet.
2. Visualize the Bending of the Magnet:
When the bar magnet is bent into the shape of a quadrant of a circular arc, the effective length of the magnet changes. The new effective length will be the straight line distance between the north and south poles of the arc.
3. Determine the Effective Length:
For a quadrant of a circle with radius r, the effective length (the straight line connecting the two ends of the arc) can be calculated using the Pythagorean theorem:
Effective Length=√(r)2+(r)2=√2r2=r√2
4. Relate the Radius to the Original Length:
The length of the arc (which is the original length L of the bar magnet) is given by the formula for the circumference of a circle:
Arc Length=πr2
Setting this equal to L:
πr2=L⟹r=2Lπ
5. Substitute the Radius into the Effective Length:
Now substitute r back into the effective length:
Effective Length=r√2=(2Lπ)√2=2L√2π
6. Calculate the New Magnetic Moment:
The new magnetic moment M′ can now be calculated using the new effective length:
M′=m⋅Effective Length=m⋅(2L√2π)
Since the original magnetic moment M=mL, we can express m as:
m=ML
Substituting this into the equation for M′:
M′=ML⋅(2L√2π)=2√2Mπ
Final Result:
Thus, the new magnetic moment M′ when the bar magnet is bent into the form of a quadrant of a circular arc is:
M′=2√2Mπ
The magnetic moment M of a bar magnet is given by the formula:
M=m⋅L
where m is the pole strength and L is the length of the magnet.
When the bar magnet is bent into the shape of a quadrant of a circular arc, the effective length of the magnet changes. The new effective length will be the straight line distance between the north and south poles of the arc.
For a quadrant of a circle with radius r, the effective length (the straight line connecting the two ends of the arc) can be calculated using the Pythagorean theorem:
Effective Length=√(r)2+(r)2=√2r2=r√2
The length of the arc (which is the original length L of the bar magnet) is given by the formula for the circumference of a circle:
Arc Length=πr2
Setting this equal to L:
πr2=L⟹r=2Lπ
Now substitute r back into the effective length:
Effective Length=r√2=(2Lπ)√2=2L√2π
The new magnetic moment M′ can now be calculated using the new effective length:
M′=m⋅Effective Length=m⋅(2L√2π)
Since the original magnetic moment M=mL, we can express m as:
m=ML
Substituting this into the equation for M′:
M′=ML⋅(2L√2π)=2√2Mπ
Thus, the new magnetic moment M′ when the bar magnet is bent into the form of a quadrant of a circular arc is:
M′=2√2Mπ
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section- C Linked Comprehension Type Questions
3 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section D (Assertion- Reason Type Questions)
8 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section - A Objective Type Questions (One option is correct)
58 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
Unit of magnetic moment is
View SolutionA magnetic wire of dipole moment 4πAm2 is bent in the form of semicircle. The new magnetic moment is
View SolutionWith reference to magnetic dipole, match the tems of Column I with the tems of Column Ii and Choose the correct option from the codes given below.

View SolutionA bar magnet of magnetic moment M is cut into four identical parts as shown in figure, then magnetic moment of each part is
_PHY_E06_282_Q01.png)
View SolutionAn iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
View SolutionA bar magnet of lenth l and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be

View SolutionA steel wire of length l has a magnetic moment M. It is bent into a semicircular arc. What is the new magnetic moment?
View SolutionA steel wire of length l has a magnetic moment M. It is bent into a semicircular arc. What is the new magnetic moment?
View SolutionA steel wire of length 'l' has a magnetic moment 'M'. It is bent in 'L' shape having equal size of arm. The new magnetic moment is
View SolutionTwo identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
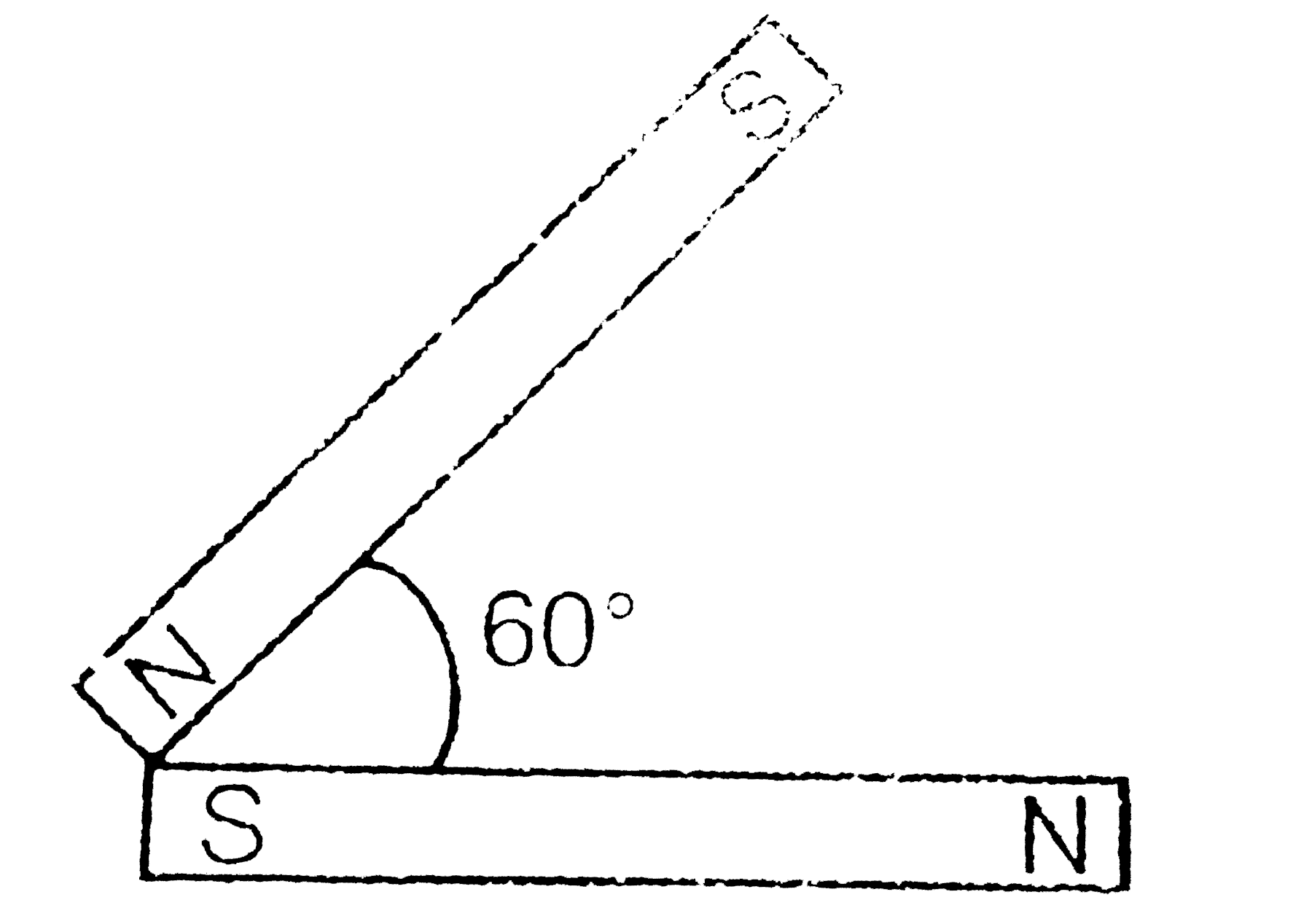
View Solution
