Two identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
2(μ04π)Md3
(μ04π)Md3
√5(μ04π)Md3
2√5(μ04π)Md3
The correct Answer is:A
To solve the problem of finding the magnetic field at point P due to two identical bar magnets, each with a magnetic moment M, we can follow these steps:
1. Understand the Configuration:
- We have two identical bar magnets placed parallel to each other. Each magnet has a magnetic moment M.
- The distance between the two magnets is 2D, and the distance from each magnet to point P is D.
2. Magnetic Field due to a Single Bar Magnet:
- The magnetic field B at a distance r from a magnetic dipole (bar magnet) with magnetic moment M is given by the formula:
B=μ04π⋅2Mr3
- Here, μ0 is the permeability of free space.
3. Calculate Magnetic Field from Each Magnet:
- For the first magnet (let's call it Magnet A), the distance to point P is D:
BA=μ04π⋅2MD3
- For the second magnet (Magnet B), the distance to point P is also D:
BB=μ04π⋅2MD3
4. Determine the Direction of the Magnetic Fields:
- Since both magnets are aligned in the same direction, the magnetic fields BA and BB at point P will add up.
5. Calculate the Total Magnetic Field at Point P:
- The total magnetic field BP at point P is the sum of the magnetic fields from both magnets:
BP=BA+BB=μ04π⋅2MD3+μ04π⋅2MD3
- This simplifies to:
BP=2⋅μ04π⋅2MD3=2μ04π⋅2MD3
6. Final Expression for the Magnetic Field:
- Therefore, the magnetic field at point P is:
BP=2μ0M2πD3=μ0MπD3
7. Select the Correct Option:
- From the options provided, we can see that the correct answer matches with option A:
BP=2⋅μ0M4πD3
- We have two identical bar magnets placed parallel to each other. Each magnet has a magnetic moment M.
- The distance between the two magnets is 2D, and the distance from each magnet to point P is D.
- The magnetic field B at a distance r from a magnetic dipole (bar magnet) with magnetic moment M is given by the formula:
B=μ04π⋅2Mr3
- Here, μ0 is the permeability of free space.
- For the first magnet (let's call it Magnet A), the distance to point P is D:
BA=μ04π⋅2MD3
- For the second magnet (Magnet B), the distance to point P is also D:
BB=μ04π⋅2MD3
- Since both magnets are aligned in the same direction, the magnetic fields BA and BB at point P will add up.
- The total magnetic field BP at point P is the sum of the magnetic fields from both magnets:
BP=BA+BB=μ04π⋅2MD3+μ04π⋅2MD3
- This simplifies to:
BP=2⋅μ04π⋅2MD3=2μ04π⋅2MD3
- Therefore, the magnetic field at point P is:
BP=2μ0M2πD3=μ0MπD3
- From the options provided, we can see that the correct answer matches with option A:
BP=2⋅μ0M4πD3
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION A)
36 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION B)
24 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section D (Assertion- Reason Type Questions)
8 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
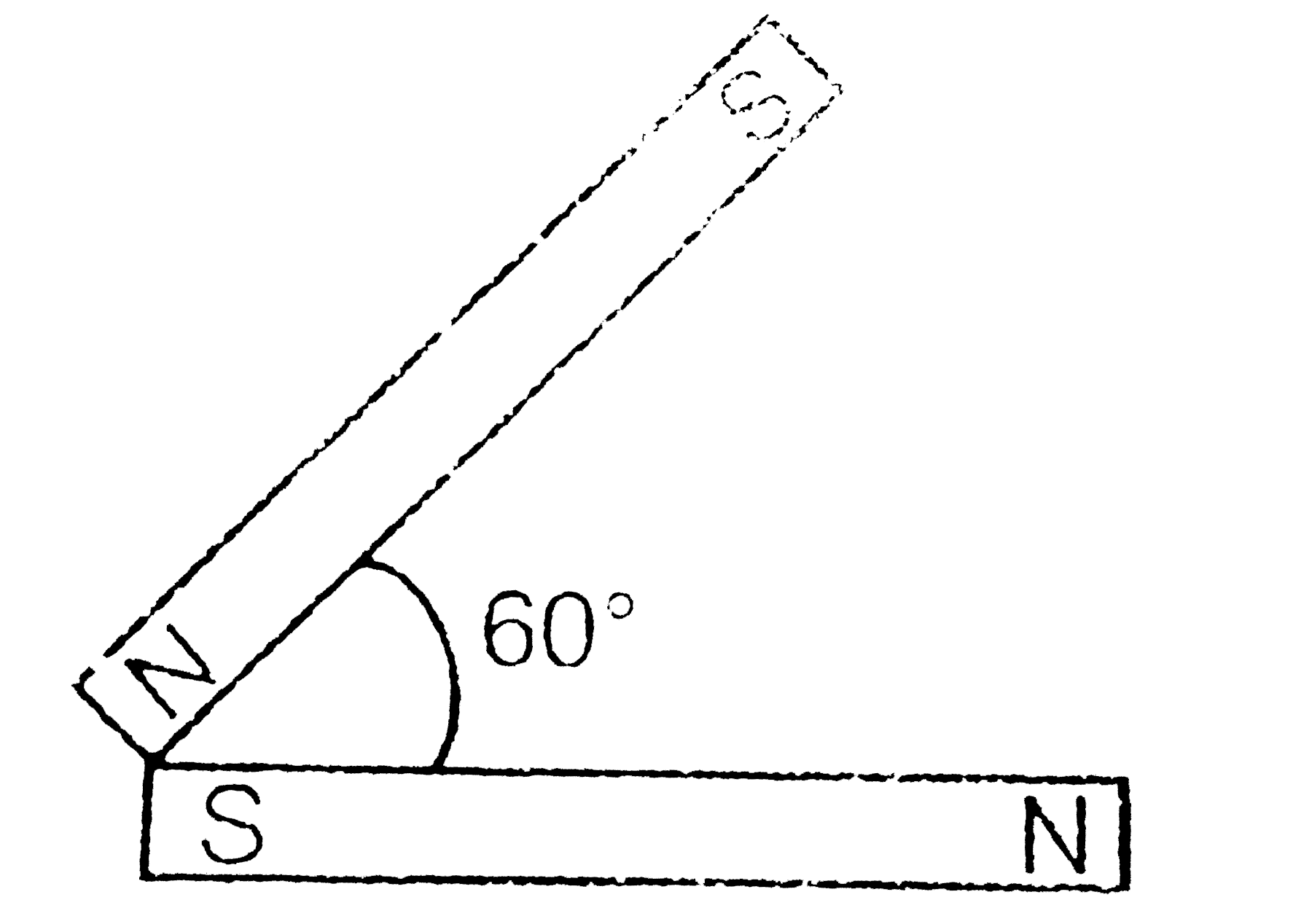
Two identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
View SolutionOrientation of two identical small bar magnet of magnetic moment 'M' is as shown in figure. The magnitude of magnetic field at the point which lies on equatorial line of one magnet and axial line of another magnet is (r >> size of magnet)
View SolutionTwo identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
View SolutionTwo identical short bar magnets of magnetic moment M each are placed at distance r apart in end-on position, then magnetic force between both is
View SolutionThree identical bar magnets each of magnetic moment M are arranged in the form of an equilateral triangle such that at two vertices like poles are in contact. The resultant magnetic moment will be
View SolutionTwo magnets of equal magnetic moments M each are placed as shown in figure below . The resultant magnetic moment is M . Then value of θ is

View SolutionThe potential enargy of bar magnet of magnetic moment 8Am2 placed in a uniform magnetic field of 2 T at an angle of 120∘ is equal to
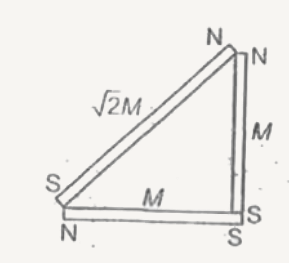
View SolutionThe magnetic moment of the arrangment shown in the figure is
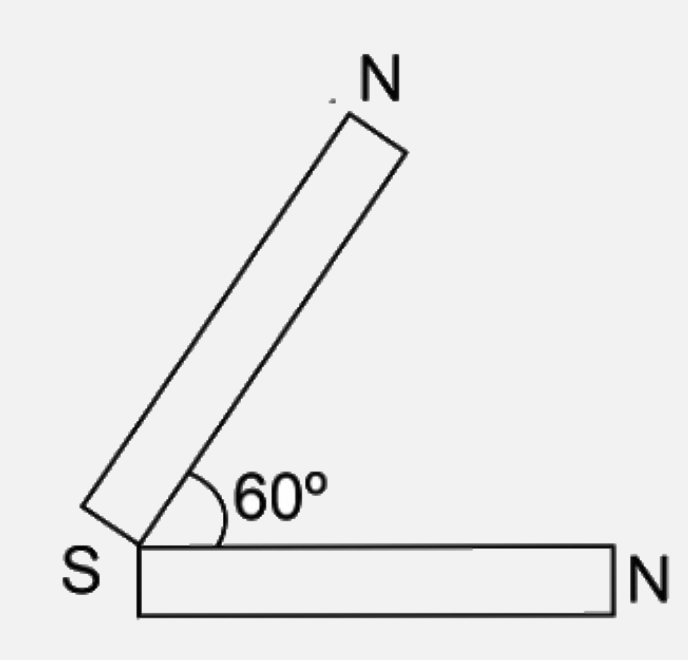
View SolutionThe net magnetic moment of the two identical magnets each of magnetic moment M0 inclined at 60∘ with each other is
View SolutionTwo identical short bar magnets are placed at 120∘ as shown in the figure. The magnetic moment of each magnet is M. Then the magnetic field at the point P on the angle bisector is given by

View Solution
