A voltmeter has a range O−V with a series resistance R. With a series resistance 2R, the range is O−V'. The correct relation between V and V'is
V'=2V
V'> 2 V
V' >> 2V
V' <2V
The correct Answer is:D
To solve the problem, we need to establish the relationship between the voltages V and V′ when the voltmeter is connected with different series resistances.
1. Understanding the Setup:
- A voltmeter is connected in series with a resistance R and measures a voltage V.
- When the series resistance is changed to 2R, the voltmeter measures a new voltage V′.
2. Current through the Voltmeter:
- Let Ig be the current flowing through the circuit when the voltmeter is connected with resistance R.
- The relationship for the current Ig when connected with resistance R is given by:
Ig=VR+G
where G is the internal resistance of the voltmeter.
3. Current with Series Resistance 2R:
- When the resistance is changed to 2R, the current I′g can be expressed as:
I′g=V′2R+G
4. Equating the Currents:
- Since the same current flows through both configurations, we have:
Ig=I′g
- Therefore, we can set the equations equal to each other:
VR+G=V′2R+G
5. Cross Multiplying:
- Cross multiplying gives:
V(2R+G)=V′(R+G)
6. Expanding and Rearranging:
- Expanding both sides:
2VR+VG=V′R+V′G
- Rearranging gives:
2VR−V′R=V′G−VG
- Factoring out common terms:
R(2V−V′)=G(V′−V)
7. Finding the Ratio:
- Dividing both sides by R and rearranging gives:
V′V=2R+GR+G
8. Final Relation:
- Thus, we can derive the relationship:
V′=2V(R+G)2R+G
Conclusion:
The correct relation between V and V′ is:
V′<2V
- A voltmeter is connected in series with a resistance R and measures a voltage V.
- When the series resistance is changed to 2R, the voltmeter measures a new voltage V′.
- Let Ig be the current flowing through the circuit when the voltmeter is connected with resistance R.
- The relationship for the current Ig when connected with resistance R is given by:
Ig=VR+G
where G is the internal resistance of the voltmeter.
- When the resistance is changed to 2R, the current I′g can be expressed as:
I′g=V′2R+G
- Since the same current flows through both configurations, we have:
Ig=I′g
- Therefore, we can set the equations equal to each other:
VR+G=V′2R+G
- Cross multiplying gives:
V(2R+G)=V′(R+G)
- Expanding both sides:
2VR+VG=V′R+V′G
- Rearranging gives:
2VR−V′R=V′G−VG
- Factoring out common terms:
R(2V−V′)=G(V′−V)
- Dividing both sides by R and rearranging gives:
V′V=2R+GR+G
- Thus, we can derive the relationship:
V′=2V(R+G)2R+G
The correct relation between V and V′ is:
V′<2V
Similar Questions
A galvanometer has range 0 − V volt and it has resistance R. When the series resistor of resistance 2R is connected, the range becomes 0 ⋅ V . Then
View SolutionA voltmeter has a resistance G and range V. Calculate the resistance to be used in series with it to extend its range to nV.
View SolutionA voltmeter has a resistance G and range V. Calculate the resistance to be used in series with it to extend its range to nV.
View SolutionA 1Ω voltmeter has range 1V find the additional resistance which has to join in series in voltmeter to increase the range of voltmeter to 100V :-
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionA voltmeter of range 2 V and resistance 300Ω cannot be converted into ammeter of range
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
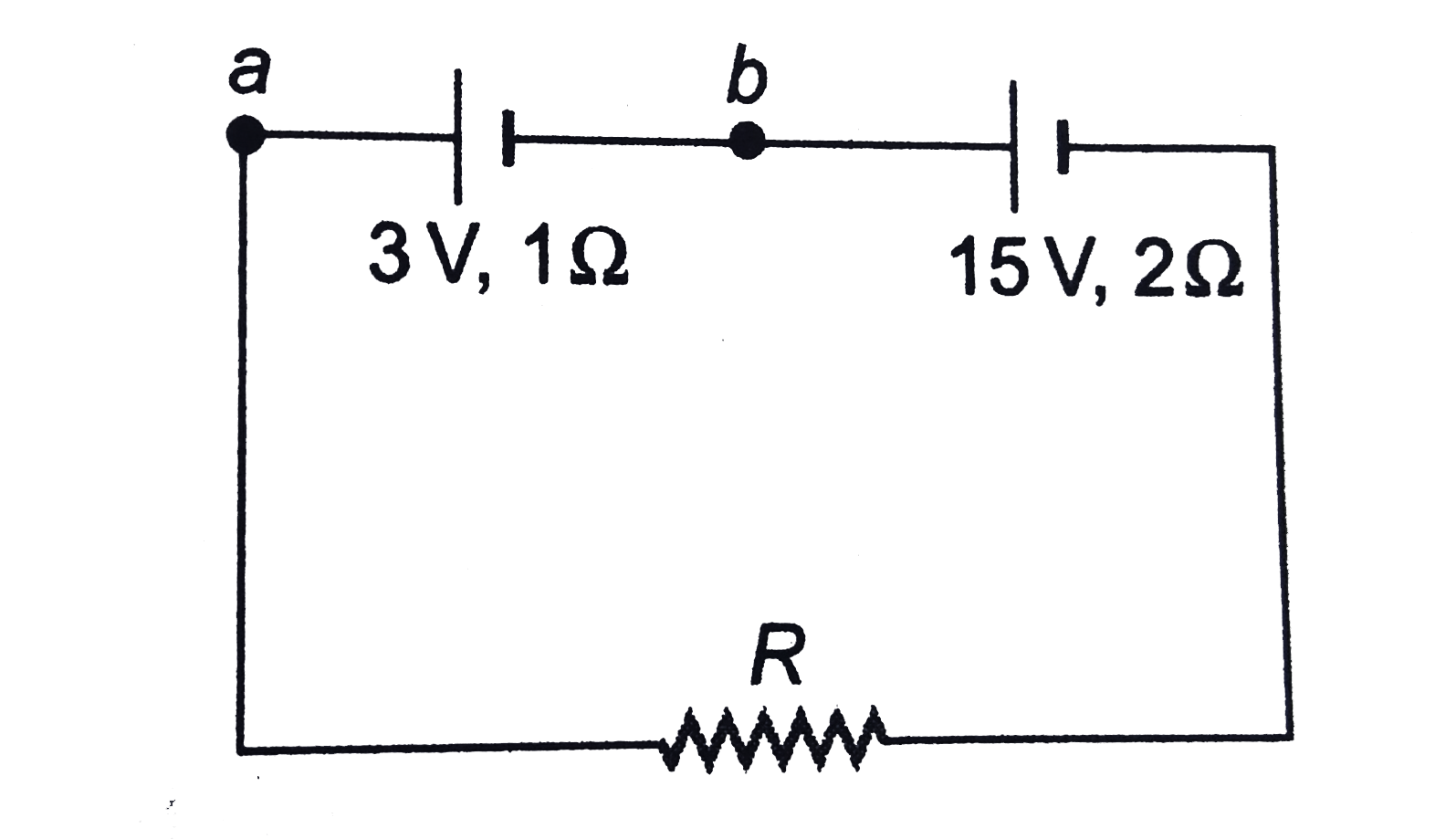
View SolutionA galvanmeter of resistance G is converted into a voltmeter of range 0 -1V by connecting resistance R1 in series with it. The additional resistance that should be connected in series with R1 to increase the range of the voltmeter to 0-2 V will be :
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View SolutionA voltmeter is connected in parallel with a variable resistance R which is in series with an ammeter and a cell as shown in the figure . For one value of R=2Ω,the reading are 0.25A and 1.0 V. What is the internal resistance of the cell ?

View Solution
