A 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
210kΩ
315kΩ
420kΩ
440kΩ
The correct Answer is:C
To solve the problem step by step, we will analyze the circuit involving the voltmeter and the external resistance R.
Step 1: Understand the Circuit
We have a voltmeter with an internal resistance r=20kΩ connected in series with a high resistance R. The entire setup is connected to a 110V power supply. The voltmeter reads 5V.
Step 2: Calculate the Current Through the Circuit
The current I flowing through the circuit can be calculated using Ohm's law. The voltage across the voltmeter is given as 5V. The formula for current is:
I=VABr
Substituting the known values:
I=5V20kΩ=520×103=2.5×10−4A
Step 3: Apply Kirchhoff's Voltage Law
According to Kirchhoff's Voltage Law, the sum of the potential differences in a closed loop must equal zero. The total voltage supplied by the battery is 110V, which is equal to the sum of the voltage drops across the internal resistance of the voltmeter and the external resistance R.
The equation can be written as:
VPQ=I⋅(r+R)=110V
Step 4: Substitute Known Values
Substituting the current I and the internal resistance r:
2.5×10−4⋅(20×103+R)=110
Step 5: Simplify the Equation
Now, we can simplify the equation:
2.5×10−4⋅(20000+R)=110
Dividing both sides by 2.5×10−4:
20000+R=1102.5×10−4=440000
Step 6: Solve for R
Now, isolate R:
R=440000−20000=420000Ω
Step 7: Convert to Kilo Ohms
Finally, convert R to kilo ohms:
R=420kΩ
Conclusion
The value of the external resistance R is 420kΩ.
We have a voltmeter with an internal resistance r=20kΩ connected in series with a high resistance R. The entire setup is connected to a 110V power supply. The voltmeter reads 5V.
The current I flowing through the circuit can be calculated using Ohm's law. The voltage across the voltmeter is given as 5V. The formula for current is:
According to Kirchhoff's Voltage Law, the sum of the potential differences in a closed loop must equal zero. The total voltage supplied by the battery is 110V, which is equal to the sum of the voltage drops across the internal resistance of the voltmeter and the external resistance R.
Substituting the current I and the internal resistance r:
Now, we can simplify the equation:
Now, isolate R:
Finally, convert R to kilo ohms:
The value of the external resistance R is 420kΩ.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
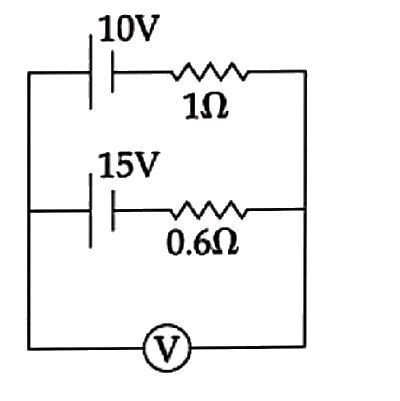
A 10 V battery with internal resistance 1Ω and a 15 V battery with internal resistance 0.6Ω are connected in parallel to a voltmeter (see figure). The reading in the voltmeter will be close to:
View SolutionA voltmeter has resistance 2000Ω and range 5 V. For increasing its range upto 20V, a resistance of
View Solution
Knowledge Check
The range of voltmeter of resistance 300Ω is 5 V. The resistance to be connected to convert it into an ammeter of range 5 A is
A1Ωin seriesB1Ωin parallelC0.1Ωin seriesD0.1Ωin parallel
A potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
View SolutionTwo batteries, one of emf 18V and internal resistance 2Ω and the other of emf 12 and internal resistance 1Ω , are connected as shown. The voltmeter V will record a reading of

View SolutionIf three uniform spheres, each having mass M and radius R, are kept in such a way that each touches the other two, the magnitude of the gravitational force on any sphere due to the other two is:
View SolutionA galvanmeter of resistance G is converted into a voltmeter of range 0 -1V by connecting resistance R1 in series with it. The additional resistance that should be connected in series with R1 to increase the range of the voltmeter to 0-2 V will be :
View SolutionThe resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
View SolutionIn the circuit shown it figure ,a voltmeter of internal resistance R, when connected across B and C reads 1003V. Neglectin the internal resistance of the battery the value of R is (5x)kΩ. Find value of x.
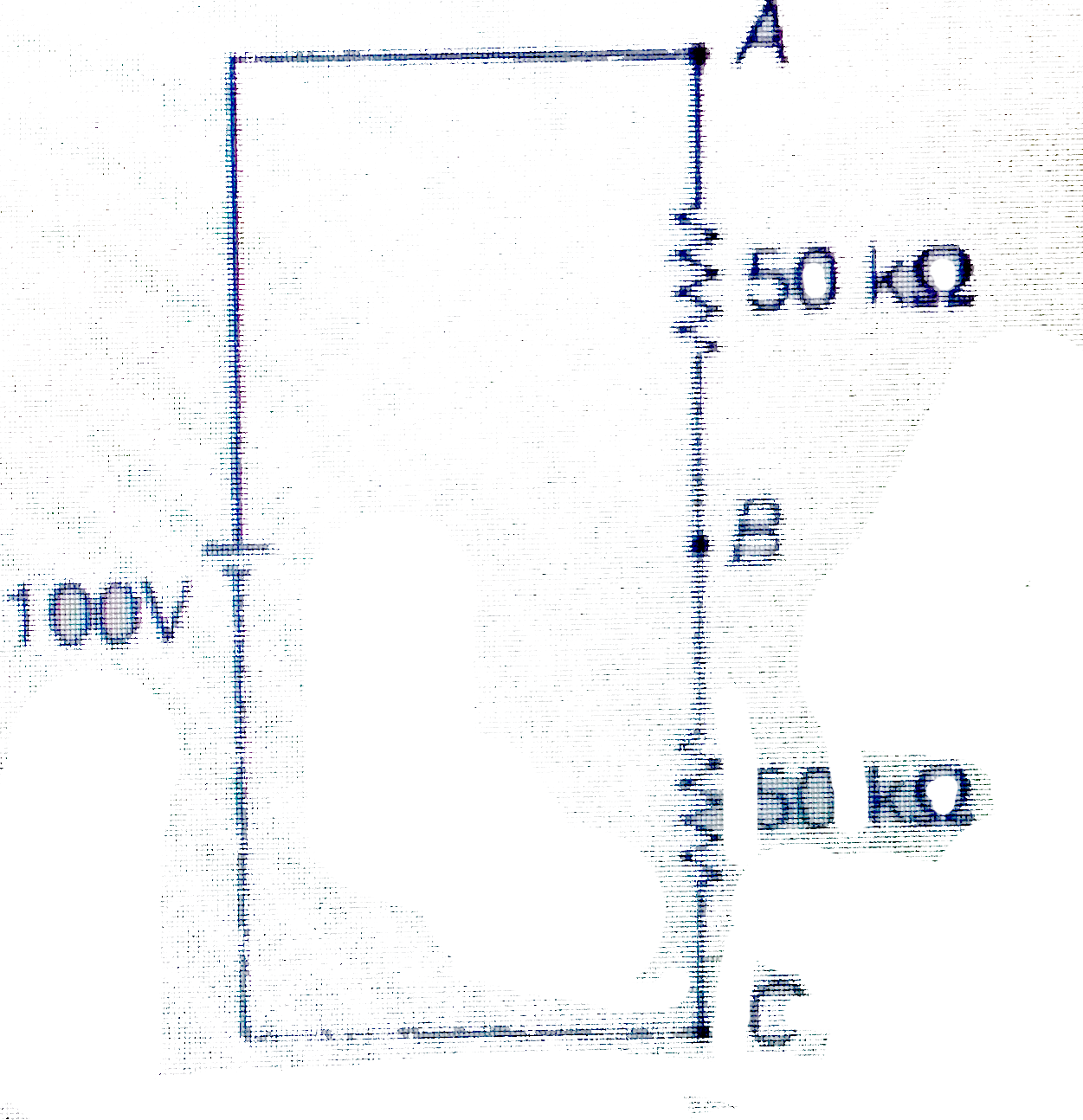
View SolutionA coil of negligible resistance is connected inseries with 90Ω resistor acorss a 120 V -60 Hz line. A voltmeter reads 36 V across the resistance. Find voltage across the coil and inductance of the coil.
View Solution
