A small block oscillates back and forth on a smooth concave surface of radius 1m. Find the time period of small oscillations.(Take g=π2ms−2)
8s
4s
2s
1s
To find the time period of small oscillations of a block on a smooth concave surface of radius 1 meter, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
The block experiences a gravitational force downward, which can be expressed as:
Fg=mg
where m is the mass of the block and g is the acceleration due to gravity.
Step 2: Identify the Components of the Gravitational Force
When the block is displaced by a small angle θ, the gravitational force can be resolved into two components:
- The component acting perpendicular to the surface: F⊥=mgcosθ
- The component acting along the surface (restoring force): F∥=mgsinθ
Step 3: Approximate for Small Angles
For small angles, we can use the approximation:
sinθ≈θ
Thus, the restoring force can be simplified to:
F∥≈mgθ
Step 4: Relate Angle to Displacement
The angle θ can be related to the displacement x from the equilibrium position using:
θ=xr
where r is the radius of the concave surface (1 m in this case).
Step 5: Substitute for the Restoring Force
Substituting θ into the expression for the restoring force gives:
F∥≈mg(xr)
Step 6: Apply Newton's Second Law
According to Newton's second law, the restoring force is also equal to mass times acceleration:
F=ma
Thus, we have:
ma=mg(xr)
Cancelling m from both sides (assuming m≠0):
a=g(xr)
Step 7: Relate Acceleration to Angular Frequency
We know that acceleration can also be expressed as:
a=ω2x
where ω is the angular frequency. Equating the two expressions for acceleration gives:
ω2x=g(xr)
Step 8: Solve for Angular Frequency
Cancelling x from both sides (assuming x≠0):
ω2=gr
Taking the square root gives:
ω=√gr
Step 9: Relate Angular Frequency to Time Period
The time period T is related to angular frequency by:
T=2πω
Substituting for ω:
T=2π√rg
Step 10: Substitute Values
Given r=1m and g=π2m/s2:
T=2π√1π2
T=2π⋅1π
T=2seconds
Final Answer
The time period of small oscillations is:
T=2seconds
---
The block experiences a gravitational force downward, which can be expressed as:
Fg=mg
where m is the mass of the block and g is the acceleration due to gravity.
When the block is displaced by a small angle θ, the gravitational force can be resolved into two components:
- The component acting perpendicular to the surface: F⊥=mgcosθ
- The component acting along the surface (restoring force): F∥=mgsinθ
For small angles, we can use the approximation:
sinθ≈θ
Thus, the restoring force can be simplified to:
F∥≈mgθ
The angle θ can be related to the displacement x from the equilibrium position using:
θ=xr
where r is the radius of the concave surface (1 m in this case).
Substituting θ into the expression for the restoring force gives:
F∥≈mg(xr)
According to Newton's second law, the restoring force is also equal to mass times acceleration:
F=ma
Thus, we have:
ma=mg(xr)
Cancelling m from both sides (assuming m≠0):
a=g(xr)
We know that acceleration can also be expressed as:
a=ω2x
where ω is the angular frequency. Equating the two expressions for acceleration gives:
ω2x=g(xr)
Cancelling x from both sides (assuming x≠0):
ω2=gr
Taking the square root gives:
ω=√gr
The time period T is related to angular frequency by:
T=2πω
Substituting for ω:
T=2π√rg
Given r=1m and g=π2m/s2:
T=2π√1π2
T=2π⋅1π
T=2seconds
The time period of small oscillations is:
T=2seconds
Similar Questions
A small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionThe ear ring of a lady shown in figure has a 3 cm long light suspension wire. A. Find the time period of small oscillations if the lady is standing on the ground. b. The lady now sits in a merry go round moving at 4ms−1 in a circle of radius 2 m. find the time period of small oscillation of the ear ring.

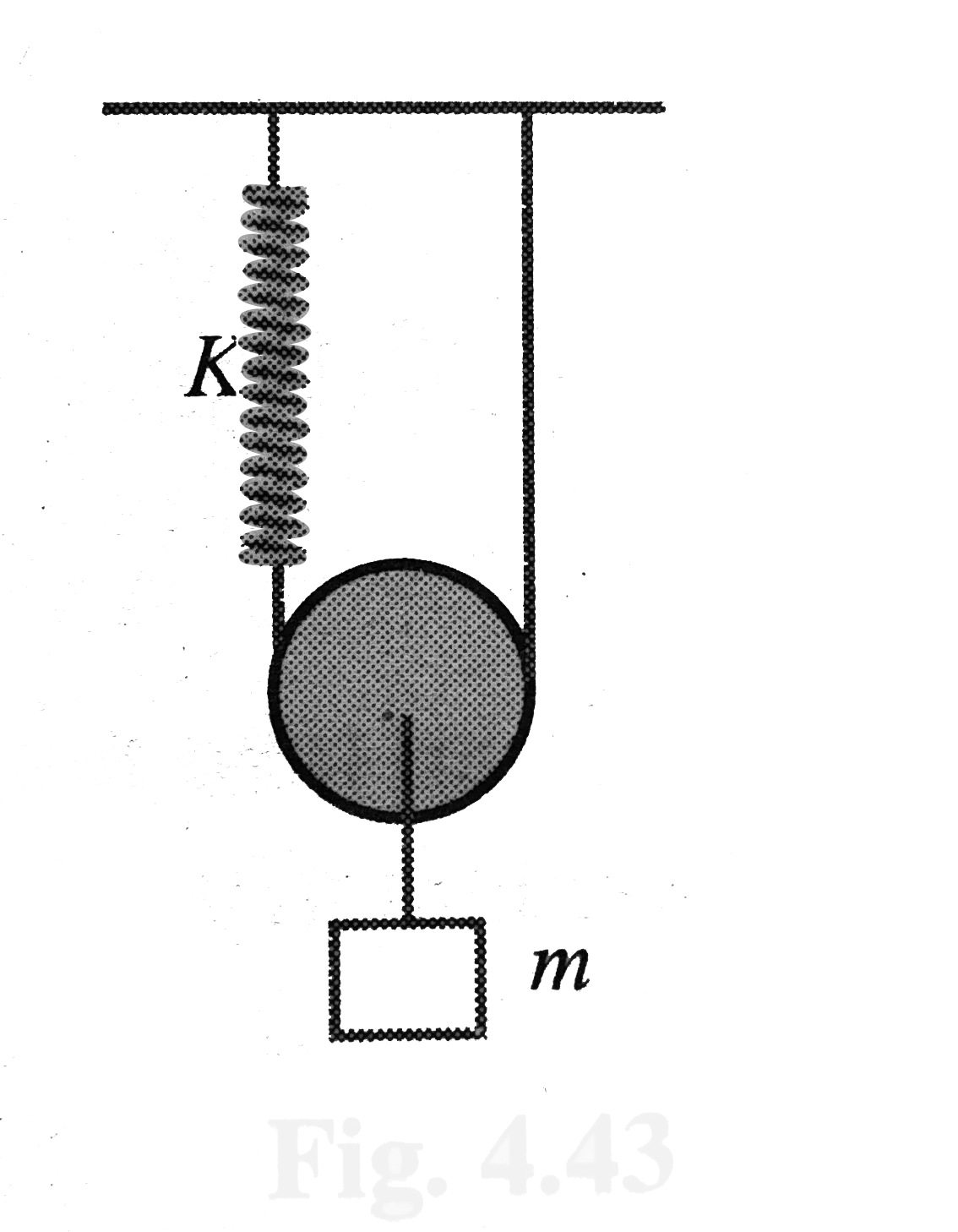
View SolutionFind the time period of m if pulley P is light and small.
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View SolutionIf a ball is dropped from height 2 metre on a smooth eleastic floor, then the time period of oscillation is
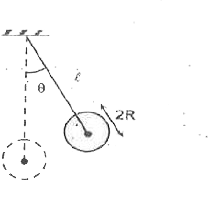
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
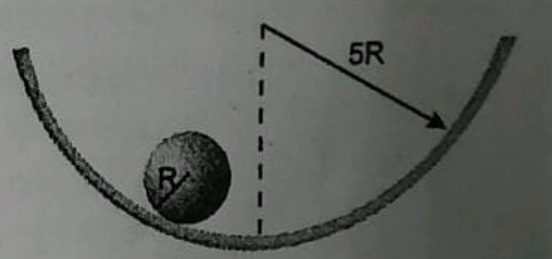
View SolutionA solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
View Solution