Find the time period of m if pulley P is light and small.
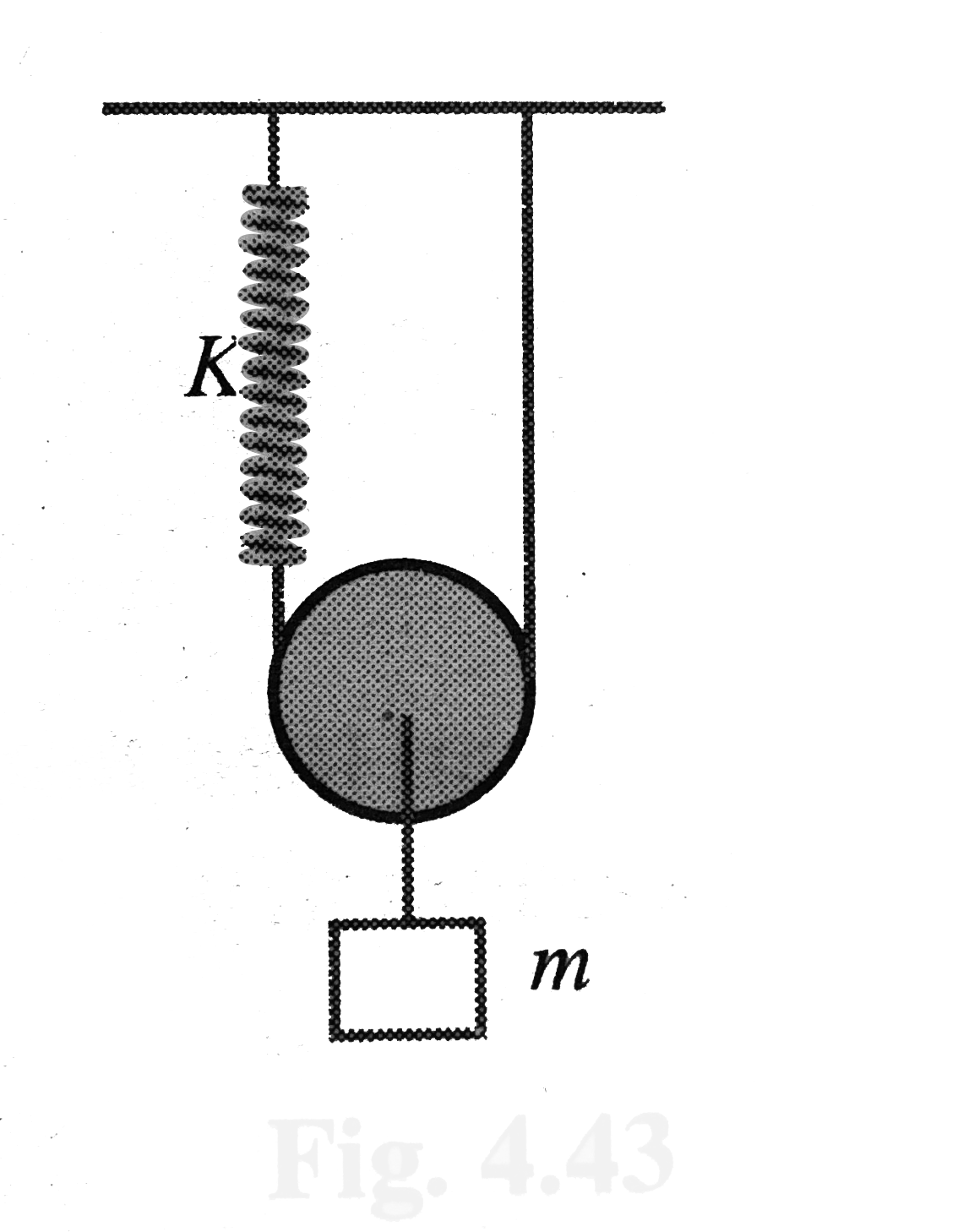
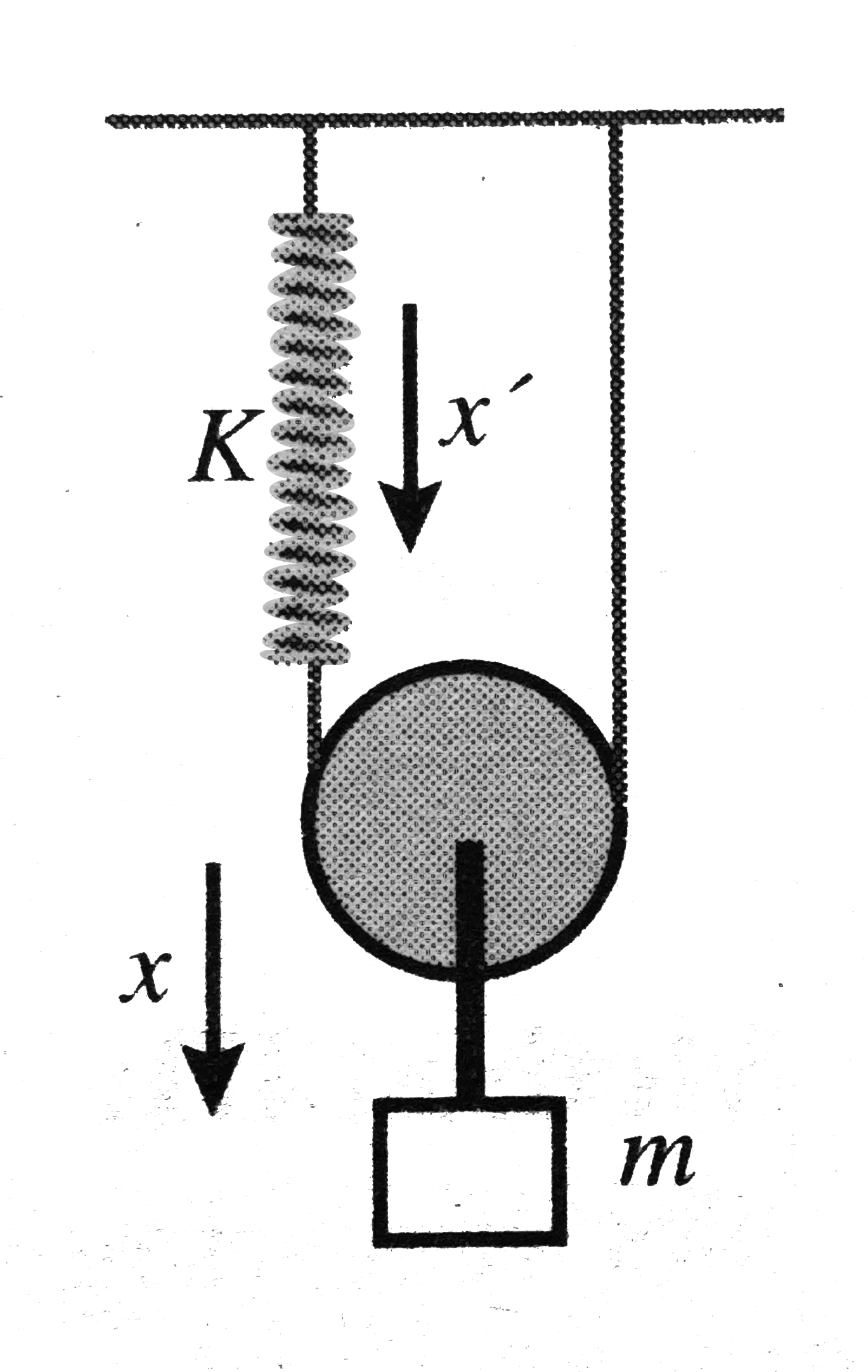
Let the displacement of block at any time be x and stretch of spring be x,, then
x'+02=x'=2x
Method I: force method
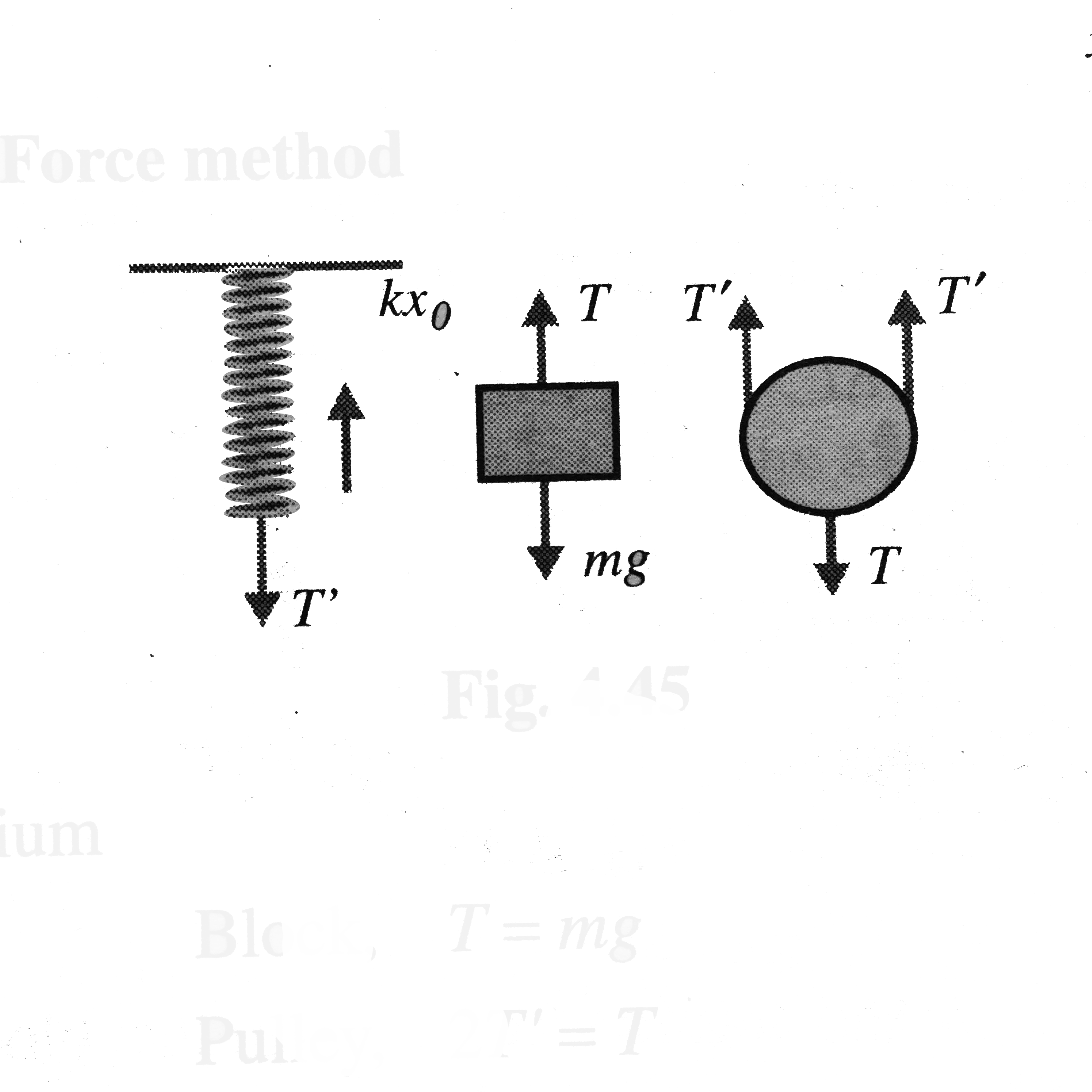
At equailibrum
Block,T=mg (i)
pulley, 2T=T (ii)
Spring, kx0=mg
Let the block is further displaced by small amount released.
Equation of motion at any time
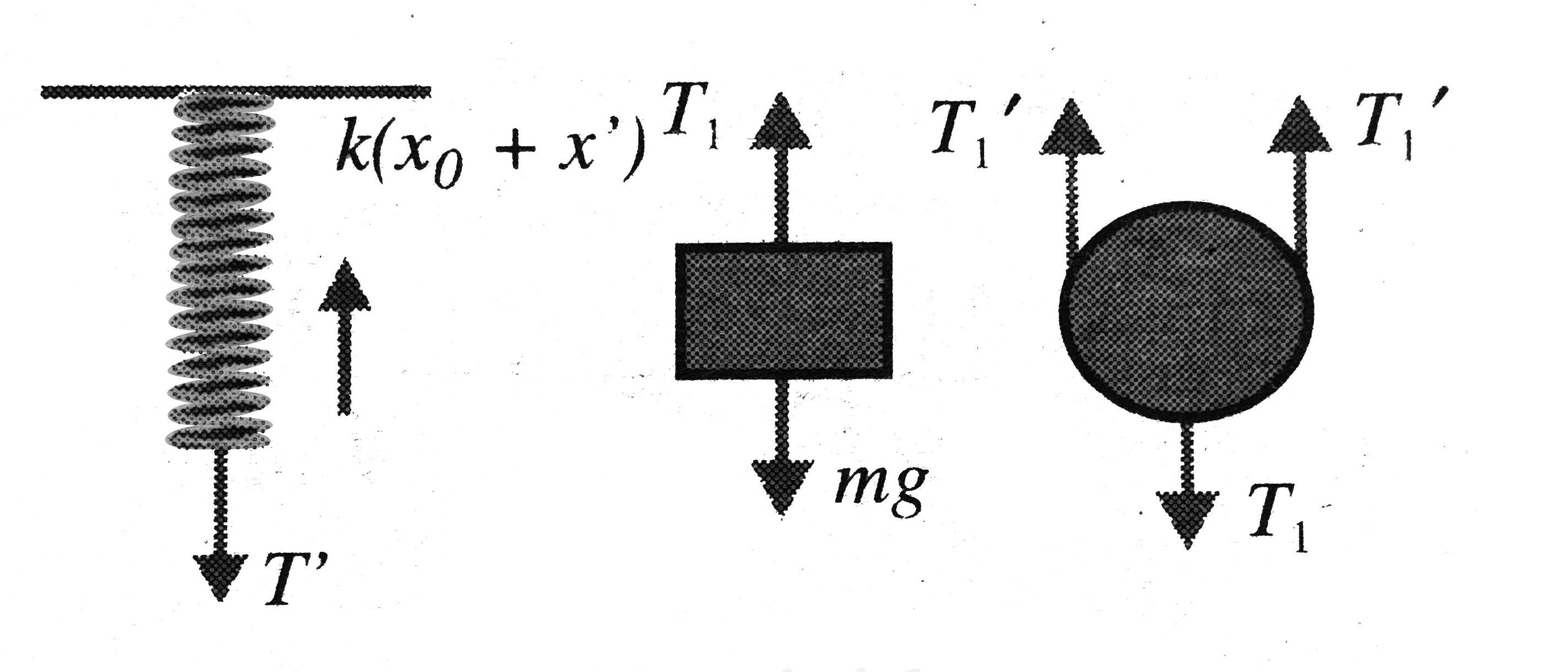
T1−mg=ma
2T1−mg=ma (ii)
2K(x0+x')−mg=ma (iii) From Eqs, (iii)and (iv)
2Kx'=ma⇒a=2Kx'm=(4km)x⇒(4km)x
ω2=4km⇒ω=√4km
Method II : Energy method
12mv2+12k(x0+x')2−mgx= constant
12m2va+12k2(x0+x')dx'dt−mg(dx)dt=0
mva+k(x0+x')dx'dt−mgv=0
mva+k(x0+2x')2v−mgv=0
ma+2k(x0+2x')−mgv=0
ma+4kx=0 (as mg=2Ks0)
a=−(4Km)x,⇒ω=√4km
Method IIi : Net resoting force on m = Net increase in tension string connecting m and pulley =ΔT
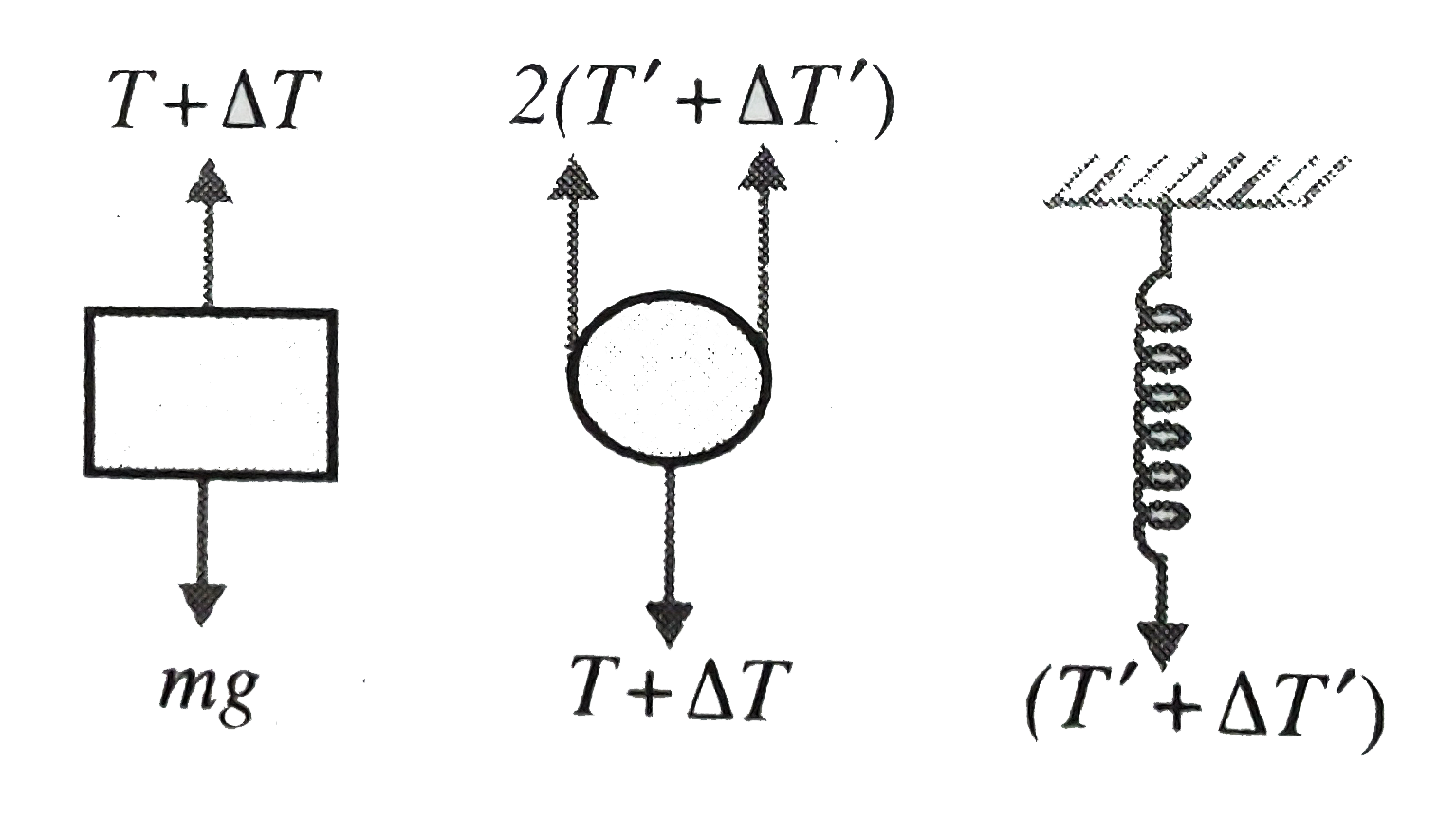
. If increase in the tension connecting the block and the pulley is ΔT, then increase in the tension connecting spring and pulley will be ΔT=ΔT/2
. If x is the displacement of the block beyond equalibrium position, then aditional stretch of spring will be x=2x
ΔT=ma⇒ΔT=ma
2kx'=4kx
a=−(4km)x⇒ω=√4km
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
The ear ring of a lady shown in figure has a 3 cm long light suspension wire. A. Find the time period of small oscillations if the lady is standing on the ground. b. The lady now sits in a merry go round moving at 4ms−1 in a circle of radius 2 m. find the time period of small oscillation of the ear ring.

View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

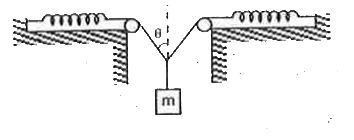
View SolutionConsider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
View SolutionTwo point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.
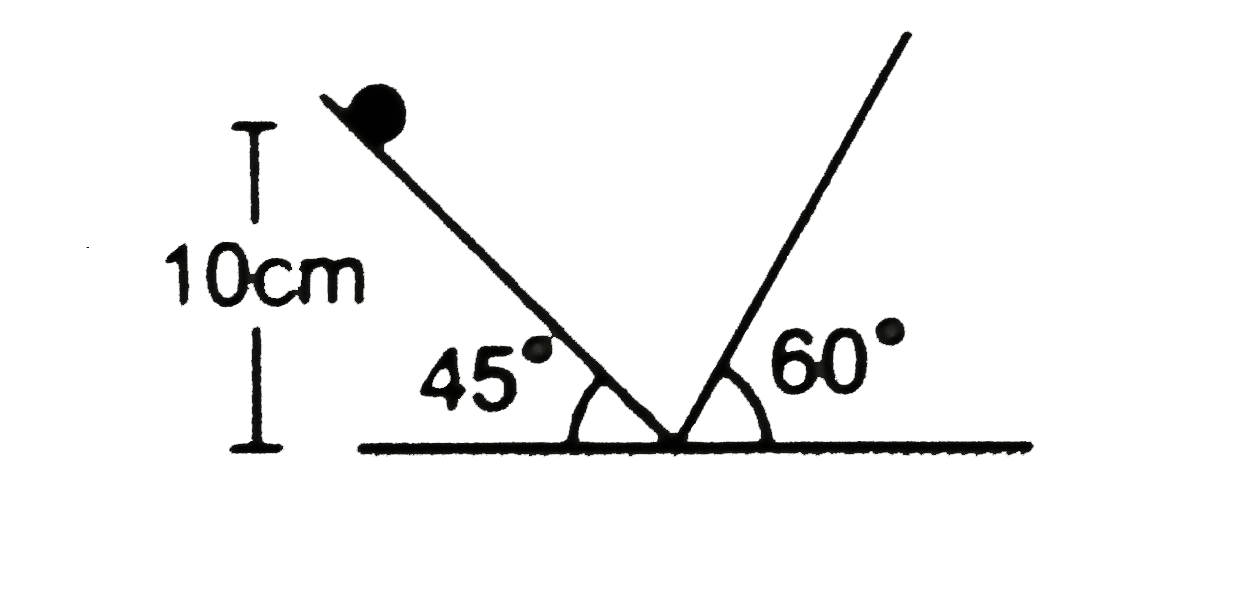
View SolutionFind the time period of the motion of the particle shown in figure. Neglected small effect of the bend near the bottom.
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
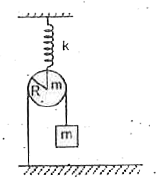
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
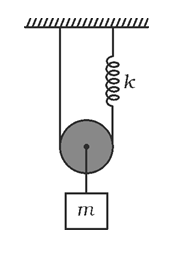
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
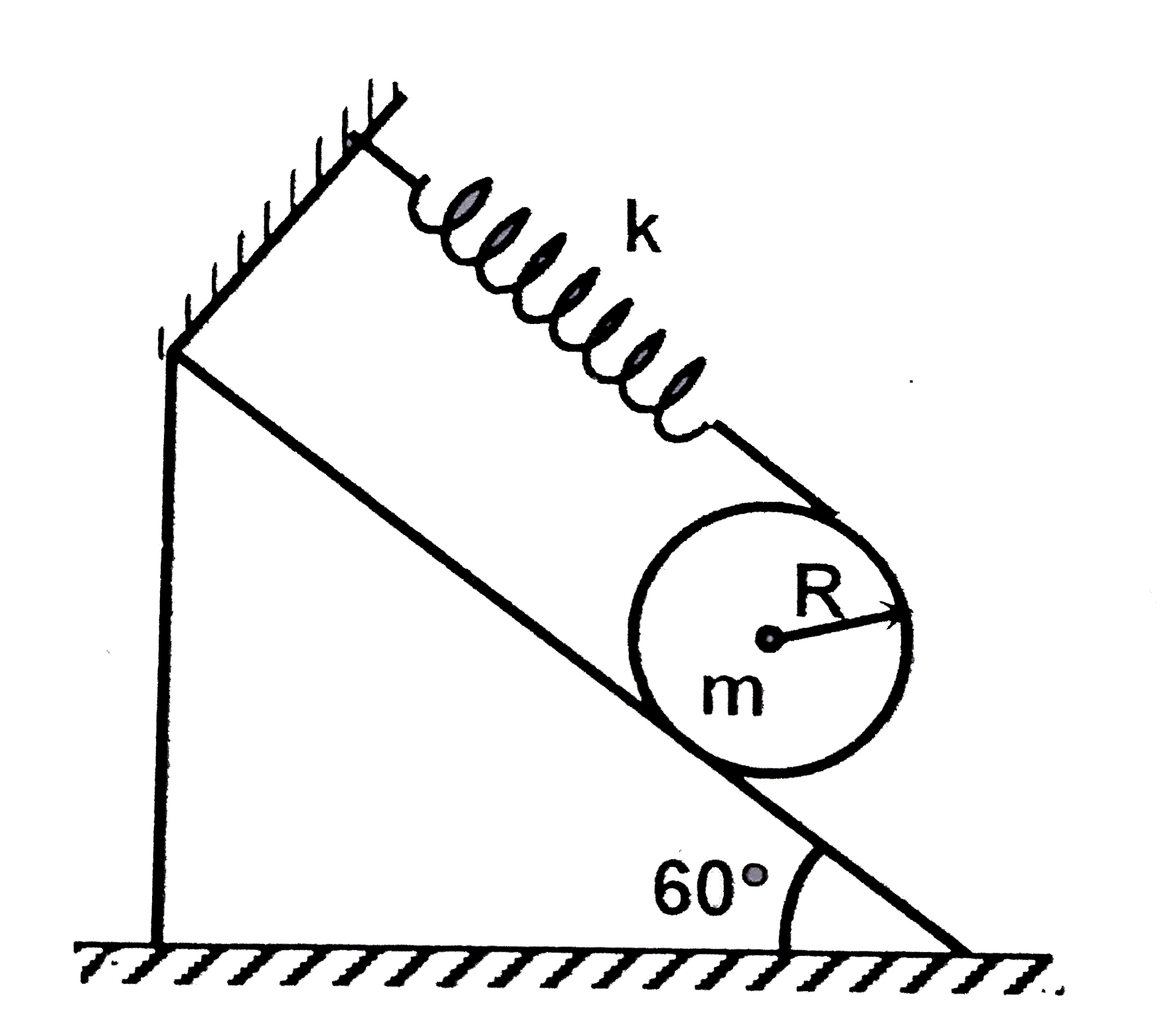
View SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
View Solution
