IF linear mass density a rod of length 2 m is changing with position as kg m then mass of the rod with one end at origin wil be
10 kg
6 kg
2 kg
12 kg
To find the mass of the rod with a linear mass density given by λ=3x+2 kg/m, we can follow these steps:
Step 1: Understand the linear mass density
The linear mass density λ is defined as the mass per unit length of the rod. In this case, it varies with position x along the length of the rod.
Step 2: Express the mass element
The mass element dm of a small segment of the rod of length dx at position x can be expressed as:
dm=λdx=(3x+2)dx
Step 3: Set up the integral for total mass
To find the total mass M of the rod, we need to integrate dm from x=0 to x=2 (the length of the rod):
M=∫20dm=∫20(3x+2)dx
Step 4: Perform the integration
Now, we can compute the integral:
M=∫20(3x+2)dx=∫203xdx+∫202dx
Calculating each part:
1. For ∫203xdx:
∫3xdx=3x22∣∣20=3(22)2−3(02)2=3⋅42=6
2. For ∫202dx:
∫2dx=2x∣∣20=2(2)−2(0)=4
Adding these results together:
M=6+4=10kg
Final Result
The mass of the rod is M=10kg.
---
The linear mass density λ is defined as the mass per unit length of the rod. In this case, it varies with position x along the length of the rod.
The mass element dm of a small segment of the rod of length dx at position x can be expressed as:
dm=λdx=(3x+2)dx
To find the total mass M of the rod, we need to integrate dm from x=0 to x=2 (the length of the rod):
M=∫20dm=∫20(3x+2)dx
Now, we can compute the integral:
M=∫20(3x+2)dx=∫203xdx+∫202dx
1. For ∫203xdx:
∫3xdx=3x22∣∣20=3(22)2−3(02)2=3⋅42=6
∫2dx=2x∣∣20=2(2)−2(0)=4
M=6+4=10kg
The mass of the rod is M=10kg.
Topper's Solved these Questions
Similar Questions
If linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View SolutionIf the linear mass density of a rod of length 3 m (lying fromy=0 toy=3m) varies as λ=(2+y)kg/m,then position of the centre of mass of the rod from y=0 is nearly at
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View SolutionLinear mass density of a rod PQ of length l and mass m is varying with the distance x (from P), as λ=m2l(1+ax)

(i) Determine the value of a
(ii) Also determine the distance of c.m. from the end P.
View SolutionThe liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png)
View SolutionLinear mass density of a rod AB(of≤n>h10m) varies with distance x from its end A as λ =λ0x3 (λ0 is positive constant) . Distance of centre of mass of the rod , from end B is
View SolutionA light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
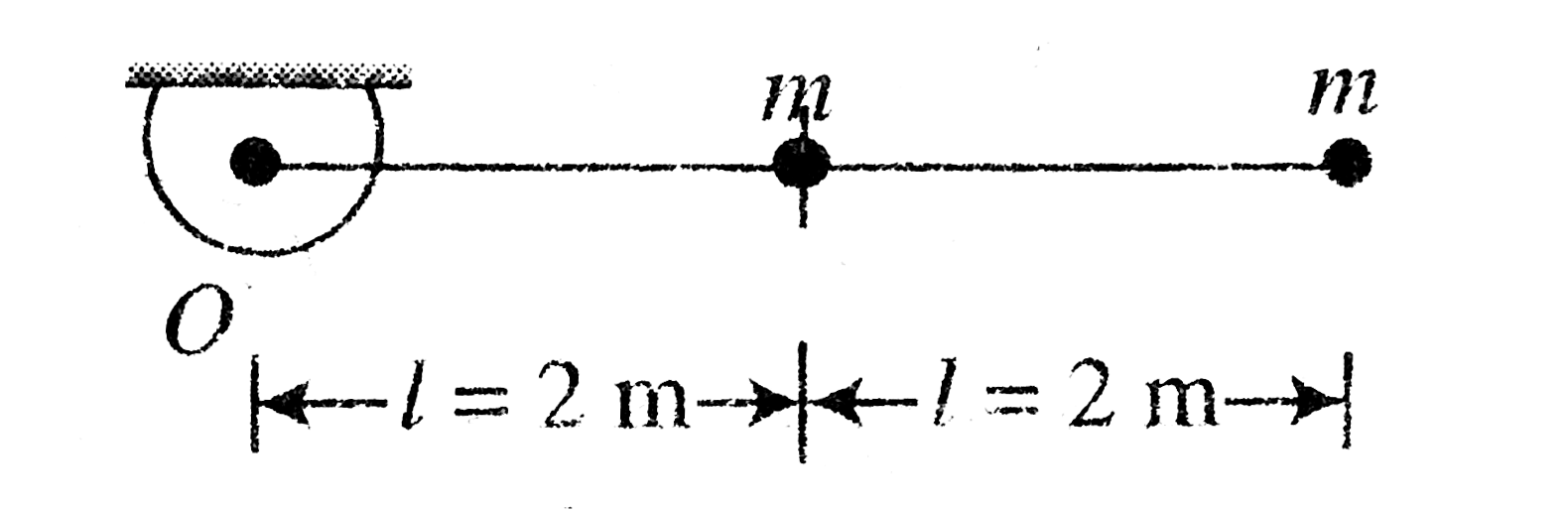
reaction offered by the pivot at t=0 (in N).
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is poitive constant). Distance of centre of mass the rod, form end B is
View SolutionThe linear mass density lambda of a rod AB is given by λ=α+βx kg/m taking O as origin. Find the location of the centre of mass from the end A?
View Solution