Particle of masses 1g, 2g, 3g…. 100g are kept at the marks 1cm. 2cm, 3cm …. 1000cm respectively on 2 meter scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale.
By adding all the masses, we get M = 5050g
= 5.050 kg
= 5.1 kg
and L = 1m
M. I of the meter scale = 5.1×1212
=0.425kgm2
=0.43kg−m2
Similar Questions
Particles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
View SolutionParticles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular besector of the metre scale.
View Solution
Knowledge Check
Two masses of 500 gram and 600 grams are attached to the 10 cm and 80 cm marks respectively of a light metre scale. The moment of inertia of this system about an axis passing through the centre of the scale will be
A0.134 kg-m2B2 kg-m2C0.56 kg-m2D4.5 kg-m2Three particles of masses 1gm,2gm&3gm are at 1cm,2cm&3cm from the axis of rotation respectively then the moment of inertia of the system & radius of gyration of the system respectively are …. gmcm2 and ….. cm
A63,2.449B60,4.5C36,4.449D36,2.449Weights of 1g, 2g,...., 100g are suspended from the 1-cm, 2-cm,......, 100-cm marks respectively of a light meter scale. Where should it be supported for the system to be in equilibrium ?
A55-cm markB60-cm markC66-cm markD72-cm mark
Particles of masses 1g, 2g, 3g, ……. 100g re kept at the marks 1 cm, 2cm, 3cm,………. 100 cm, respectively on a metre scale. Find the moment of inertia of the system of particle about a perpendicular bisector of the metre scale.
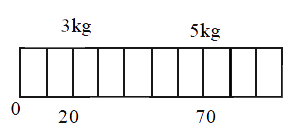
View SolutionTwo masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is
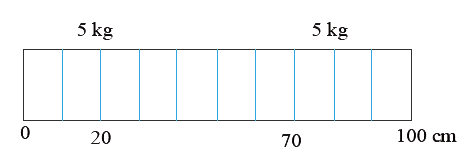
View SolutionTwo masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is

View SolutionTwo masses of 3kg and 5kg are placed at 20cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passing through 100 cm mark and perpendicular to the meter scale is
View SolutionThree particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.
View Solution
