Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of $a \times b$

Text Solution

Verified by Experts

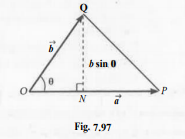
Let $\to a$ represented by $- - \to O P$ and $\to b$ be represented by $- - \to O Q$ .
Let $∠ P O Q = θ$

Complete the gm OPRQ join PQ.
Draw $O N ⊥ O P$
In $Δ O Q N, sin θ = \frac{Q N}{O Q} = \frac{Q N}{b}$
$Q N = b sin θ$
Now, by definition, $∣ ∣ \to a \times \to b ∣ ∣$
$= a b sin θ = (O P) (Q N)$
$= \frac{2 (O P) (Q N)}{2} = 2 \times area of Δ O P Q$
$∴$ area of $Δ O P Q = \frac{1}{2} ∣ ∣ \to a \times \to b ∣ ∣$ , which was to be proved.

Updated on:21/07/2023

Given $θ$ be the angle between unit vectors A and B Then, |AxxB| is equal to
A $sin θ$
B $cos θ$
C $tan θ$
D $cot θ$
The area of a triangle formed by the sides of vector $\to A and \to B$ is
A $∣ ∣ \to A \times \to B ∣ ∣$
B $∣ ∣ \to A \cdot \to B ∣ ∣$
C $\frac{1}{2} ∣ ∣ \to A \cdot \to B ∣ ∣$
D $\frac{1}{2} ∣ ∣ \to A \times \to B ∣ ∣$