Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
Show P=P−i+miV
Where Pi is the momentum of the ii the particle (of mass mi) and p'i+miv'i− Note v'i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass ∑P'i=0
Let m1,m2,….mi mass points have the position vectors →r1,→r2,→ri w.r.t origin .O..
The position vector of C.M say −−→OP
i.e., −−→OP=m1→r1+m2→r2+....m1+m2+....=miriM
where i=1,2,3.
Now, let us change the origin to O. and assume that the C.M is now at p. with
−−−−→O.P.=m1r11+m2r12+...M=mir1iM
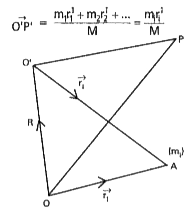
Where r11,r21...r1i are the position vectors of masses m1,m2,....mi w.r.t origin O.
From fig. −−→OO.+−−−→O.A=−−→OAor→R+−→r.i=→ri−(1)
Multiplying eqn. (1) by mi and diffirentiating w.r.t to time, we get
mid→Rdt+mid−→r.idt=mi=d→ridt
mi→V+mi−→V1i=mi→Vi
miv+p.i=pi
And −−−−→O.P.=mi(→ri−R)M=−−→OP−R−(2)[∵ from (1)]
But from Δle OO.P, we have
−−→OO.+−−−→O.P=−−→OPorR+−−−→O.P=−−→OP
and −−−→O.P=−−→OP−R−(3)
from (2) and (3), −−−−→O.P.=−−−→O.P
even if we change the origin, the position of centre of mass will not change i.e., ∑P.i=0
Similar Questions
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show P=Pi+miV
where pi is the momentum of the ith particle (of mass mi) and pi=mivt Notevi is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑pt=0
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles. K' is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r't×p't is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r'i=ri−R, rest of the notation is the standard notation used in the chapter. Note L' and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τext is the sum of all external torques acting on the system about the centre of mass.
(Hint : Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
View SolutionSeparation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a)n Show →p=→pi+mi→V where →pi is the momentum of the ith particle (of mass mi) and →pi=mi→vi, Not →vi is the velocity of the ith particle relative to the centre ofmass.
Also, prove using the definition of the centre of mass ∑→pi=0
(b) Show K=K'+1/2MV2 where K is the total kinetic energy of the system of particles, K is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system)
(c) Show →L=→L+→R×MV
where →L'=∑→ri×→pi is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember →ri=→ri−→R, reat of the notation is the standard notation used in the chapter. Note →L'andM→R×→V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show d→Ldt=∑→ri×d→p'dt Further show that d→L'dt=→τext' where Text is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton's Third Law. Assume the internal forces between any two particles aet along the line joining the particles.)
View Solution
Knowledge Check
Two particles of masses m and 3m approach each other with different velocities. After collision, the particle of mass m has velocity →v in their centre of mass frame. Velocity of particle of mass 3m in the centre of mass frame is
A−2→vB−→v2C−→v3D→v4A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
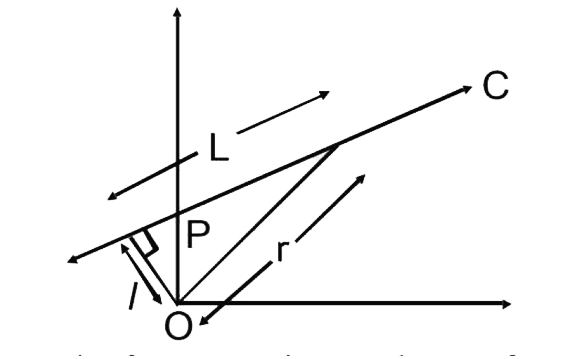 AmvLBmvICmvrDzero
AmvLBmvICmvrDzeroA particle of mass m has a velocity −v0i, while a second particle of same mass has a velocity v0j. After the particles collide, first particle is found to have a velocity −12v0¯i then the velocity of othe particle is
A−12v0→i+v0→jB12v0→i+v0→jCv0→i+v0→jD−v0→i+v0→j
If two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionWrite an expression for the position vector of the centre of mass of n-particle system. Also write the equations of motion which govern the motion of the centre of mass
View SolutionParticles of masses 1kg and 2kg are at (i+2j+3k) m and (−2i+4j+2k)m then instantaneous position of their centre of mass is
View SolutionIf there particles, each of mass M, are placed at the three corners of an equilibrium triangle of side, a the force exerted by this system on another particle of mass M placed (i) at the midpoint of side and (ii) at the centre of the triangle are, respectively.
View Solution
