Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
Show
Where is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember , rest of the notation is the standard notation used in the chapter. Note L' and can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
From eq. (1), we have
[ multiplying on both sides by M]
[ multiplying on both sides by ]
Similar Questions
Knowledge Check
- Question 1 - Select One
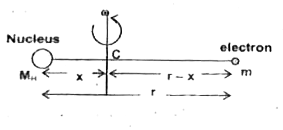
The angular momentum of the atom about the centre of mass will beAmr2ωBm(r−X)2ωC(MH+M)r2ωMHm2DMHmMH+mr2ω - Question 2 - Select One
The motion of the centre of mass is the result of
AAttractive forcesBRepulsive forcesCExternal forcesDInternal forces - Question 3 - Select One
The sum of moments of masses of all the particle in a system about the centre of mass is always
AzeroBmaximumCinfiniteDminimum

The angular momentum of the atom about the centre of mass will beView SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show P=Pi+miV
where pi is the momentum of the ith particle (of mass mi) and pi=mivt Notevi is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑pt=0
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles. K' is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r't×p't is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r'i=ri−R, rest of the notation is the standard notation used in the chapter. Note L' and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τext is the sum of all external torques acting on the system about the centre of mass.
(Hint : Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)View SolutionSeparation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a)n Show →p=→pi+mi→V where →pi is the momentum of the ith particle (of mass mi) and →pi=mi→vi, Not →vi is the velocity of the ith particle relative to the centre ofmass.
Also, prove using the definition of the centre of mass ∑→pi=0
(b) Show K=K'+1/2MV2 where K is the total kinetic energy of the system of particles, K is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system)
(c) Show →L=→L+→R×MV
where →L'=∑→ri×→pi is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember →ri=→ri−→R, reat of the notation is the standard notation used in the chapter. Note →L'andM→R×→V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show d→Ldt=∑→ri×d→p'dt Further show that d→L'dt=→τext' where Text is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton's Third Law. Assume the internal forces between any two particles aet along the line joining the particles.)View SolutionMotion Of Centre Of Mass
View SolutionMotion OF centre OF mass
View Solution
