What is the moment of inertia of a ring about a tangent to the circle of the ring?

Text Solution

Verified by Experts

The tangent to the ring in the plane of the ring is parallel to one of the diameters of the ring. The distance between these two parallel axes is R, the radius of the ring. Using the parallel axes theorem.

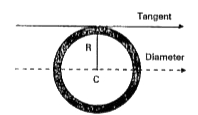
$I_{tangent} = I_{dia} + M R^{2} = \frac{M R^{2}}{2} + M R^{2} = \frac{3}{2} M R^{2}$
I = M.I. of fly wheel about its axis = $\frac{M R^{2}}{2}$
$= \frac{20.0 \times {(0.2)}^{2}}{2}$
$= 0.4 k g m^{2}$
$α$ = angular acceleration
= 5.0 Nm/0.4 kg $m^{2} = 12.5 S^{- 2}$
(b) Work done by the pull unwinding 2m of the cord
$= 25 N \times 2 m = 50 J$
(c ) Let $ω$ be the final angular velocity. The kinetic energy gained = $\frac{1}{2} I ω^{2}$
since the wheel starts from rest. Now,
$ω_{2} = ω_{0}^{2} + 2 α θ, ω_{0} = 0$
The angular displacement $θ$ = length of unwound string / radius of wheel = 2m / 0.2 m = 10 rad
$ω^{2} = 2 \times 12.5 \times 10.0 = 250 {(rad/s)}^{2}$
$∴$ K.E. gained $= \frac{1}{2} \times 0.4 \times 250 = 50 J$
(d) The answers are the same, i.e., the kinetic energy gained by the wheel work done by the force. There is no loss of energy due to friction.

Updated on:21/07/2023

Moment of inertia of a ring about a tangent to the circle of the ring is
A $\frac{2}{5} M R^{2}$
B $\frac{2}{3} M R^{2}$
C $\frac{3}{2} M R^{2}$
DNone of these
A ring and a disc have same mass and same radius. Ratio of moments of inertia of the ring about a tangent in its plane to that of the disc about its diameter is
A $2 : 1$
B $4 : 1$
C $6 : 1$
D $8 : 1$
Two identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
A $3 M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{4} M R^{2}$
D $2 M R^{2}$