Obtain an equation for the frequency of oscillation of spring of force constant k to which a mass m is attached.
Let us consider a spring suspended vertically from a rigid support and loaded with a mass m. If it is now pulled down and released, it executes vertical oscillations about mean position.
Restoring force is directly proportional to the displacement, but oppositely directed
F∝−y
F=−ky −(1)
Where k is force constant
Ma=−ky (∵F=Ma)
a=−(KM)y −(2)
Since K and M are constant. We can write a∝=−y
i.e. Acceleration is directly proportional to the displacement but oppositely directed. Hence oscillations of a loaded spring is S.H.M.
Comparing eq. (2) with a−ω2y
ω2=KM,ω=√KM
T=2πω,T=2π√KM
Frequency of oscillation (n)=12π√KM −(3)

Similar Questions
Comparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View Solution
Knowledge Check
The period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
A9:16B25:16C25:9D16:9Comparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
ACLBV1CLCCLDLCA spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
A2 nBn/√2CnD√2n
A body of mass 1 kg oscillates on a spring of force constant 16 N/m. Calculate the angular frequency.
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
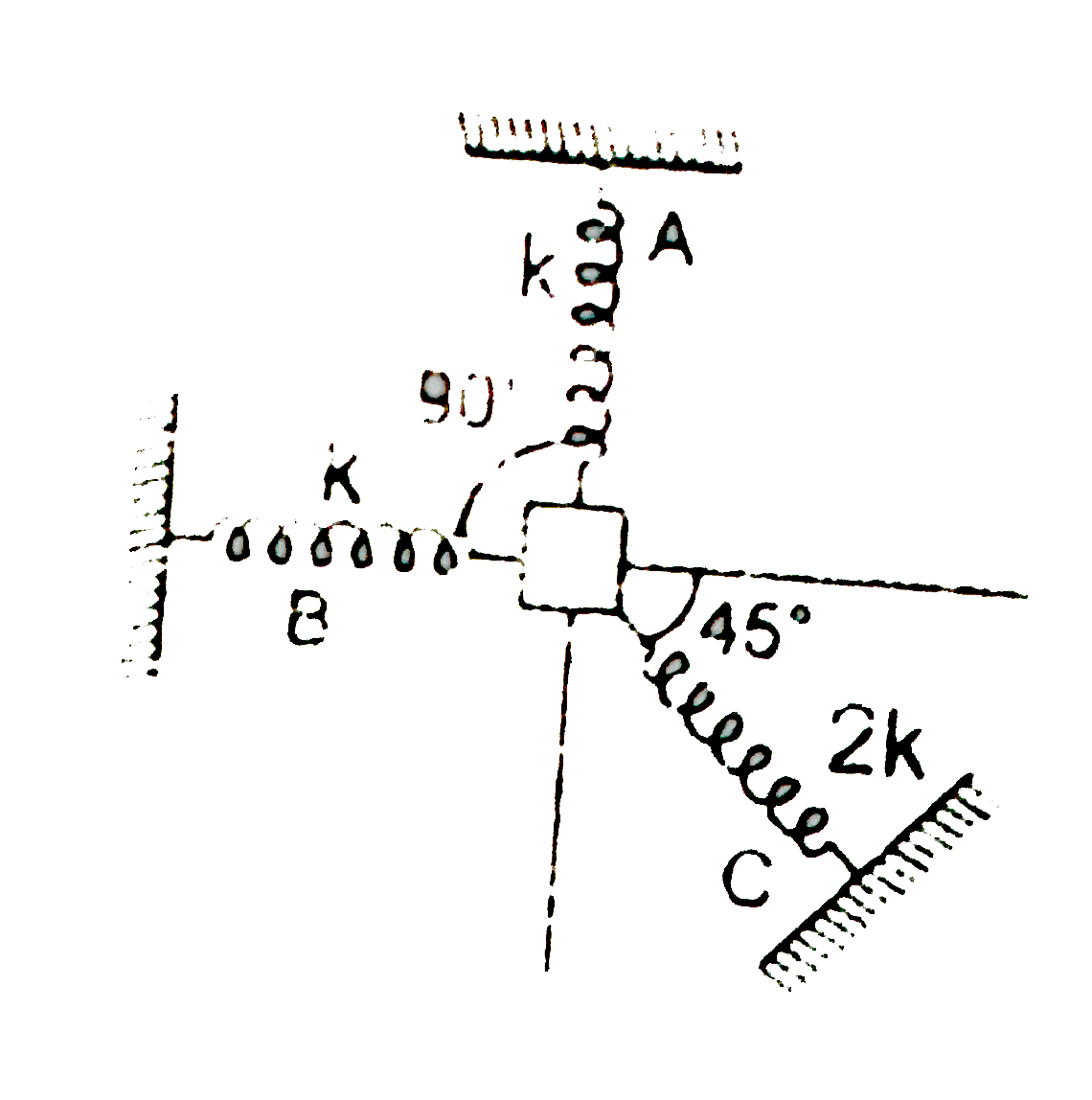
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
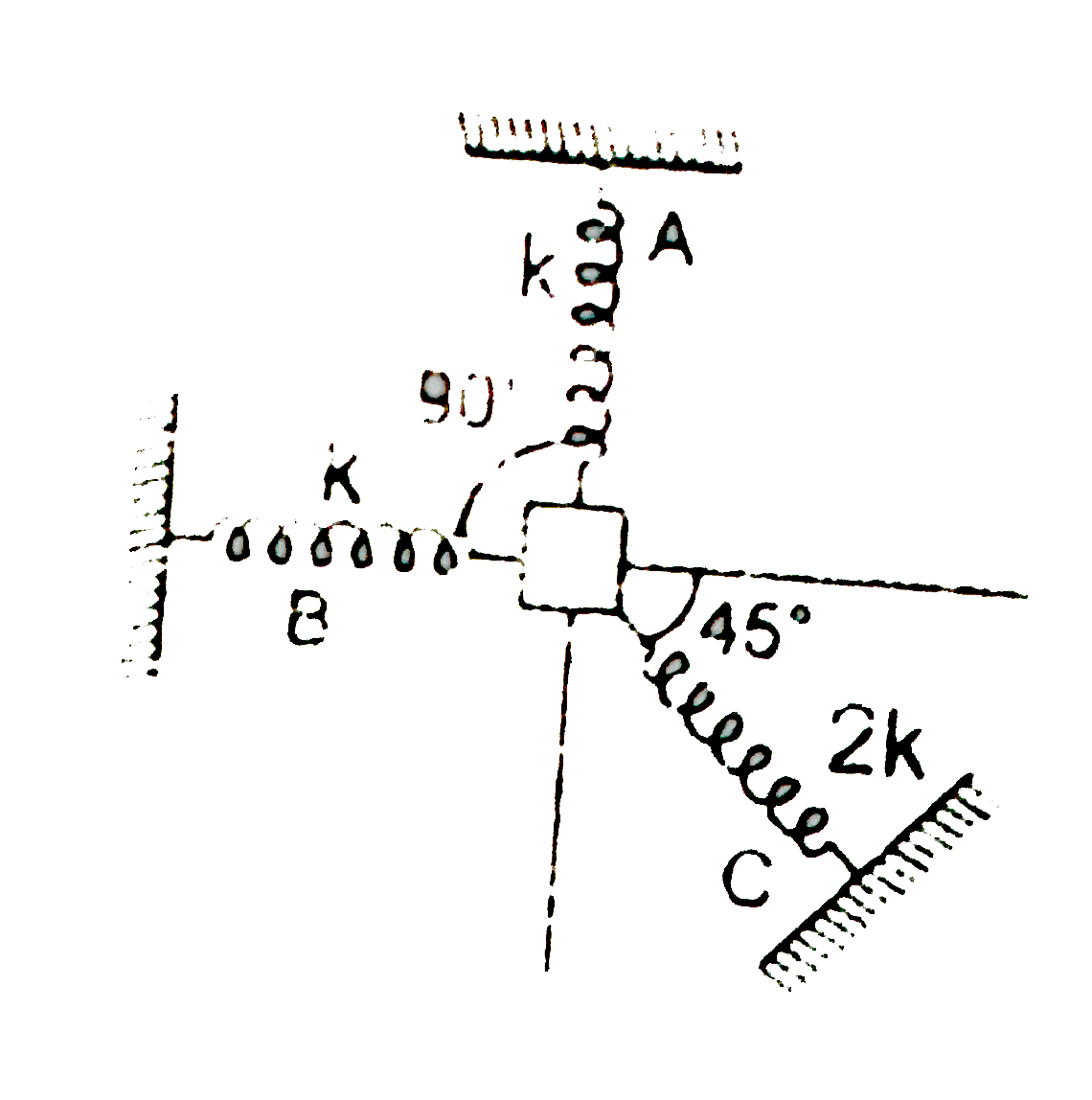
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View Solution
