A mild steel wire of length 1.0 m and cross-sectional area 0.50×10−2cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the mid-point.
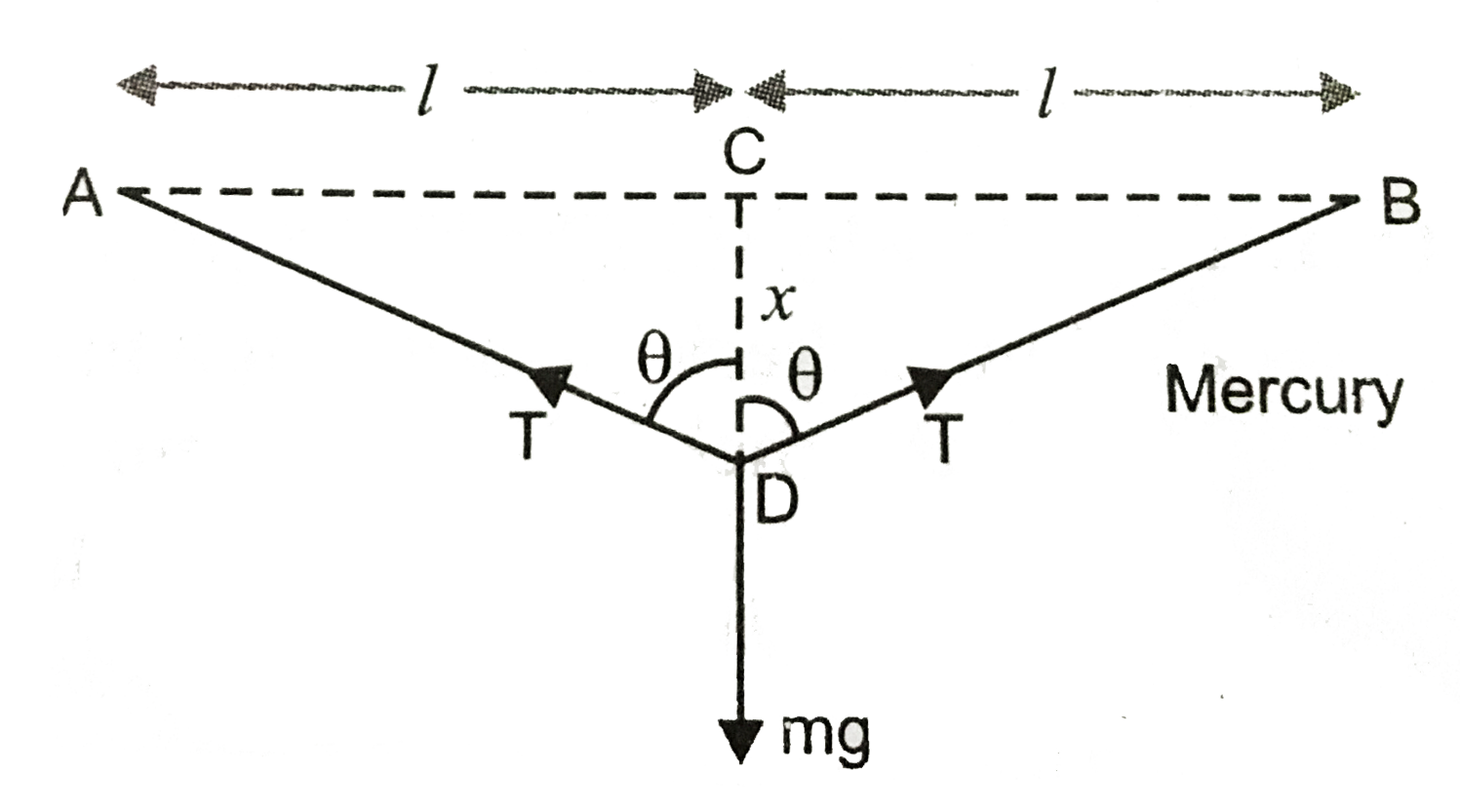
Refer the figure, let x be the depression at the mid point i.e., CD=x
In fig. AC=CB=l=0.5m
m=100g=0.100kg
AD=BD=(l2+x2)1/2
Increase in length, Δl=AD+DB−AB
=2AD−AB
=2(l2+x2)1/2−2l
=2l(1+x2l2)1/2−2l
=2l(1+x22l2)−2l=x2l
Strain=Δl2l=x22l2
If T is the tension in the wire, then 2T cosθ
=mgorT=mg2cosθ

Here, cosθ=x(l2+x2)1/2
=x(1+x2l2)1/2=xl(1+12x2l2)
As x<<1, so 1>>12x2l2and1+12x2l2=1
∴cosθ=xl
Hence, T=mg2(n/l)=mgl2x
Stress=TA=mgl2Ax
Y=StressStrain=mgl2Ax×2l2x2=mgl3Ax3
∴x=l(mgYA)1/3
=0.5(0.1×102×1011×0.5×10−6)1/3
=1.074×10−2m=1.074m.
Similar Questions
A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
View SolutionA mild steel wire of length 1.0 m and cross-sectional are 0.5×10−2cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=20×1011Nm−2.

View Solution
Knowledge Check
A mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
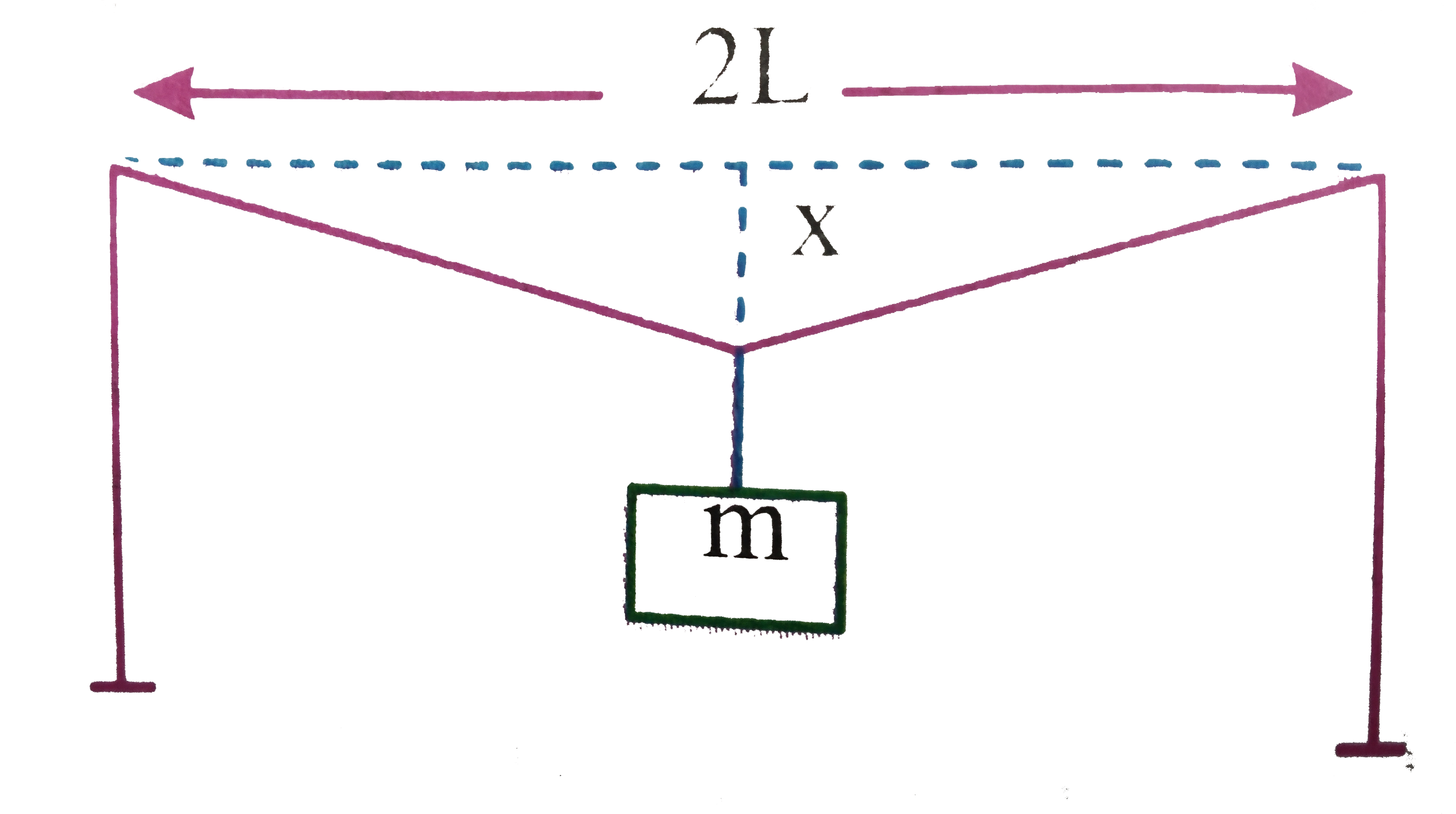 Ax22L2BxLCx2/LDx2/2L
Ax22L2BxLCx2/LDx2/2LA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
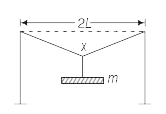 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
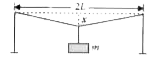
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22L
A mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is

View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View Solution
