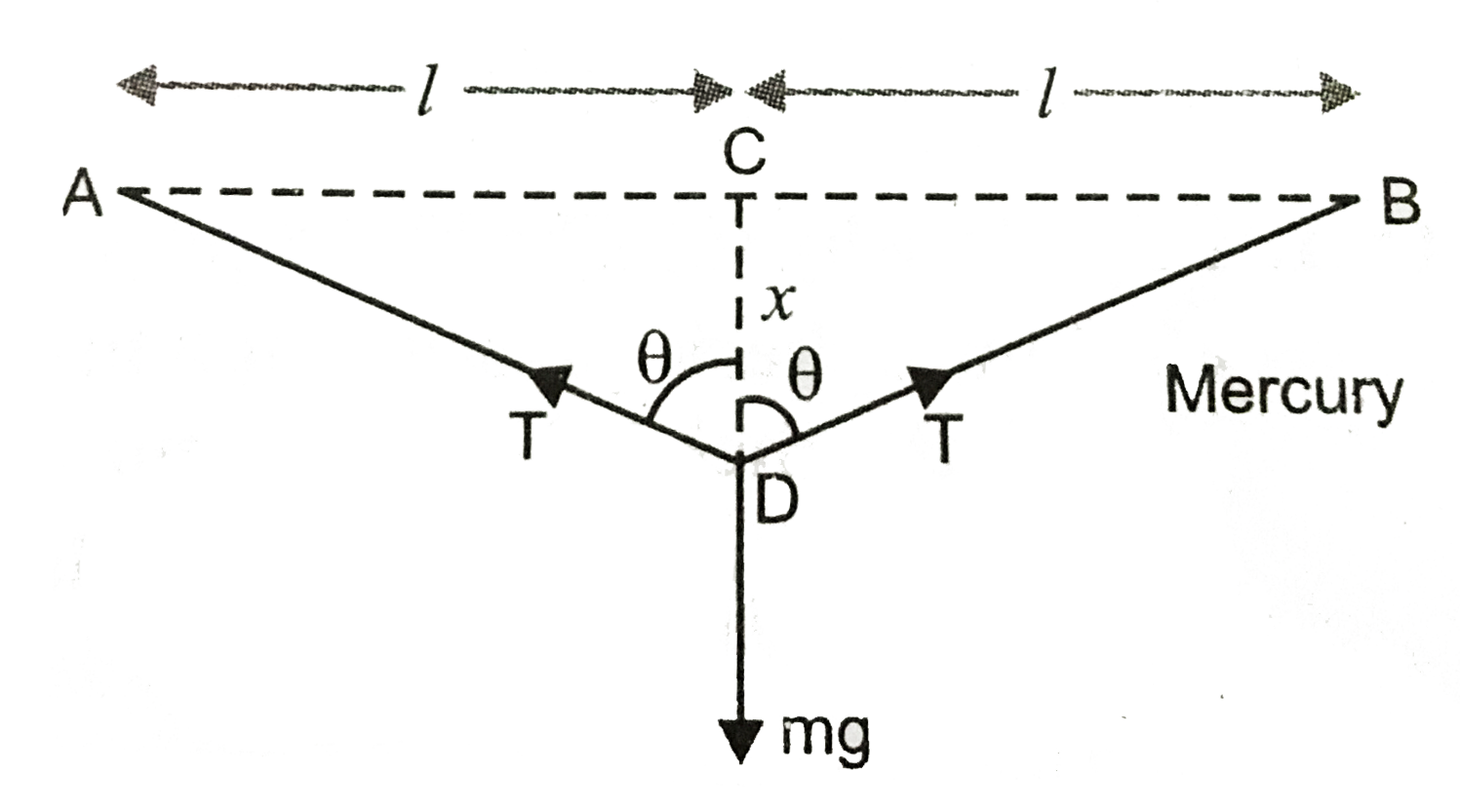
A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to
X2/L
X/L
X2/L2
X/L2
To solve the problem, we need to find how the strain in the steel wire is proportional to the depression X at the midpoint when a mass m is suspended from it.
1. Understanding the Setup:
- We have a steel wire of length 2L stretched horizontally between two pillars.
- A mass m is suspended from the midpoint of the wire, causing a depression X at that point.
2. Identifying the Lengths:
- The total length of the wire is 2L.
- When the mass is suspended, the wire forms two segments, each of length L (from the pillars to the midpoint).
- The new length of each segment when the mass is suspended can be calculated using the Pythagorean theorem. The length from the pillar to the midpoint becomes √L2+X2.
3. Calculating the Change in Length (ΔL):
- The original length of each segment is L.
- The new length of each segment is √L2+X2.
- Therefore, the change in length for each segment is:
ΔL=√L2+X2−L
- Since there are two segments, the total change in length for the wire is:
ΔLtotal=2(√L2+X2−L)
4. Calculating Strain:
- Strain (S) is defined as the change in length divided by the original length:
S=ΔLtotalLoriginal=2(√L2+X2−L)2L=√L2+X2−LL
5. Simplifying the Expression:
- We can simplify the expression for strain:
S=√L2+X2−LL
- To further simplify, we can multiply the numerator and denominator by the conjugate:
S=(√L2+X2−L)(√L2+X2+L)L(√L2+X2+L)=X2L(√L2+X2+L)
6. Finding Proportionality:
- As X increases, the strain S is proportional to X2L when L is constant.
- Thus, we can conclude that the strain in the wire is proportional to X2.
Final Answer:
The strain in the wire is proportional to X2.
- We have a steel wire of length 2L stretched horizontally between two pillars.
- A mass m is suspended from the midpoint of the wire, causing a depression X at that point.
- The total length of the wire is 2L.
- When the mass is suspended, the wire forms two segments, each of length L (from the pillars to the midpoint).
- The new length of each segment when the mass is suspended can be calculated using the Pythagorean theorem. The length from the pillar to the midpoint becomes √L2+X2.
- The original length of each segment is L.
- The new length of each segment is √L2+X2.
- Therefore, the change in length for each segment is:
ΔL=√L2+X2−L
- Since there are two segments, the total change in length for the wire is:
ΔLtotal=2(√L2+X2−L)
- Strain (S) is defined as the change in length divided by the original length:
S=ΔLtotalLoriginal=2(√L2+X2−L)2L=√L2+X2−LL
- We can simplify the expression for strain:
S=√L2+X2−LL
- To further simplify, we can multiply the numerator and denominator by the conjugate:
S=(√L2+X2−L)(√L2+X2+L)L(√L2+X2+L)=X2L(√L2+X2+L)
- As X increases, the strain S is proportional to X2L when L is constant.
- Thus, we can conclude that the strain in the wire is proportional to X2.
The strain in the wire is proportional to X2.
Topper's Solved these Questions
Similar Questions
A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
View SolutionA mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View Solution
Knowledge Check
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
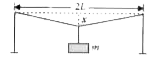
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22LA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
Ax22L2BxLCx2LDx22LA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
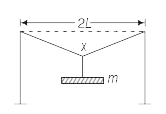 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22L
A steel wire of original length 1 m and cross-sectional area 4.00 mm^2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ?
Yofthesteel=2.0x10^11Nm^-2. Take g=10ms−2
View SolutionA steel wire having cross-sectional area 2 mm^(2) is stretched by 20 N. Find the lateral strain produced in the wire Y_("steel") = 2 xx 10^(11) Nm^(-2), sigma = 0.391
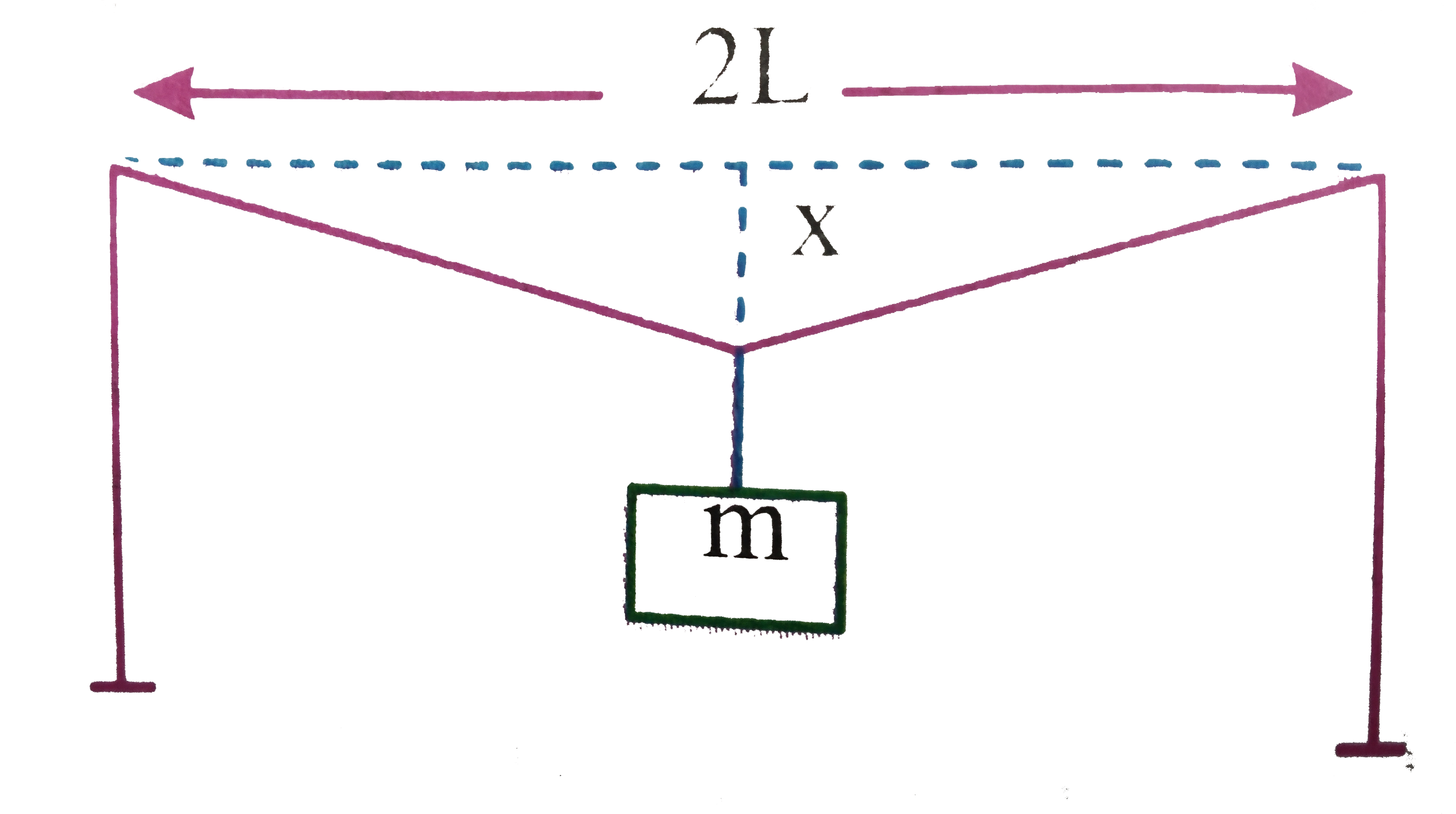
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
View SolutionA wire of cross section A is stretched horizontally between two clamps located 2lm apart. A weight Wkg is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance x<1 the strain produced is
View SolutionA steel wire having cross-sectional area 2 mm^(2) is stretched by 20 N. Find the lateral strain produced in the wire
View Solution