In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
Step by step video & image solution for In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : angleADC is greater than angleADB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - MID- POINT THEOREM9videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - PYTHAGORAS THEOREM5videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES2videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution10videos
CHAPTERWISE REVISION (STAGE 1)
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)12videos
CIRCLE
Similar Questions
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
CB:BA=CP:PAView SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
AB×BC=BP×CAView SolutionIn a triangle ABC , AB = AC and ∠A=36∘ If the internal bisector of angle C meets AB at D . Prove that AD = BC.
View SolutionIn a △ABC the sides BC=5,CA=4 and AB=3. If A(0,0) and the internal bisector of angle A meets BC in D (127,127) then incenter of △ABC is
View SolutionIn a triangle ABC, side AC is greater than side AB and point D lies on side BC such that AD bisects angle BAC. Show that:
∠ADB is acute.View SolutionLet triangle ABC be an isosceles with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Measure of the angle A in degrees, is :
View SolutionIn the given figure, AB = AC. Prove that AF is greater than AE.
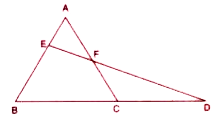 View Solution
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionThe given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.View Solution

