The given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD

Step by step video & image solution for The given figure shows an equilateral triangles ABC and D is point in AC. Prove that : (i) AD lt BD (ii) BC gt BD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - MID- POINT THEOREM
9 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - PYTHAGORAS THEOREM
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
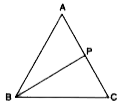
In the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC

View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

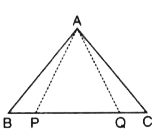
View SolutionThe given figure shows a ΔABC in which AB =AC and BP =CQ .
Prove that :
(i) ΔABQ≅ΔACP.
(ii) ΔAPQ is isosceles.
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

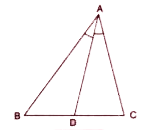
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View Solution