In triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
tan C .
The correct Answer is:113
To solve the problem, we will follow these steps:
1. Draw Triangle ABC: We have a right triangle ABC where angle B = 90°. We know that AB = 40 and AC + BC = 80.
2. Assign Variables: Let AC = x. Then, BC can be expressed as BC = 80 - x.
3. Apply the Pythagorean Theorem: According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC). Therefore, we can write:
AB2+BC2=AC2
Substituting the known values:
402+(80−x)2=x2
4. Simplify the Equation: Now, we will simplify the equation:
1600+(80−x)2=x2
Expanding (80−x)2 using the formula a2−2ab+b2:
1600+(6400−160x+x2)=x2
This simplifies to:
8000−160x+x2=x2
5. Cancel x² and Rearrange: The x2 terms on both sides cancel out:
8000−160x=0
Rearranging gives:
160x=8000
6. Solve for x: Dividing both sides by 160:
x=8000160=50
7. Find BC: Now that we have AC = x = 50, we can find BC:
BC=80−AC=80−50=30
8. Calculate tan C: We need to find tanC:
tanC=ABBC=4030=43
Thus, the final answer is:
tanC=43
AB2+BC2=AC2
Substituting the known values:
402+(80−x)2=x2
1600+(80−x)2=x2
Expanding (80−x)2 using the formula a2−2ab+b2:
1600+(6400−160x+x2)=x2
This simplifies to:
8000−160x+x2=x2
8000−160x=0
Rearranging gives:
160x=8000
x=8000160=50
BC=80−AC=80−50=30
tanC=ABBC=4030=43
tanC=43
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CO-ORDINATE GEOMETRY6videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - GRAPHICAL SOLUTION3videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - SOLIDS6videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution10videos
CHAPTERWISE REVISION (STAGE 1)
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)12videos
CIRCLE
Similar Questions
In triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
sin AView SolutionIn triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
cos AView SolutionIn triangle ABC,∠ABC−90∘,AB=2a+1andBC=2a2+2a. Find AC in terms of 'a' if a= 8 , find the lengths of the sides of the triangles.
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View SolutionThe following figures shows a right - angled triangle ABC with ∠B=90∘,AB=15 cm and AC = 25 cm. D is a point in side BC and CD = 7 cm. if De ⊥AC, find the length of DE.
 View Solution
View SolutionIn triangle ABC , ∠ABC=90∘,∠CAB=x∘,tanx∘=34andBC=15cm. Find the measures of AB and AC.
View SolutionIn ΔABC,∠C=90∘,AB=20andBC=12.D is a point in side AC such that CD = 9 Taking angle BDC = x, find
tanx−cosx+3sinx.View SolutionIn ΔABC,∠C=90∘,AB=20andBC=12.D is a point in side AC such that CD = 9 Taking angle BDC = x, find
sin∠ABCView SolutionIn the figure, in ΔABC,∠B=90∘,AB=28cmandBC=21cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
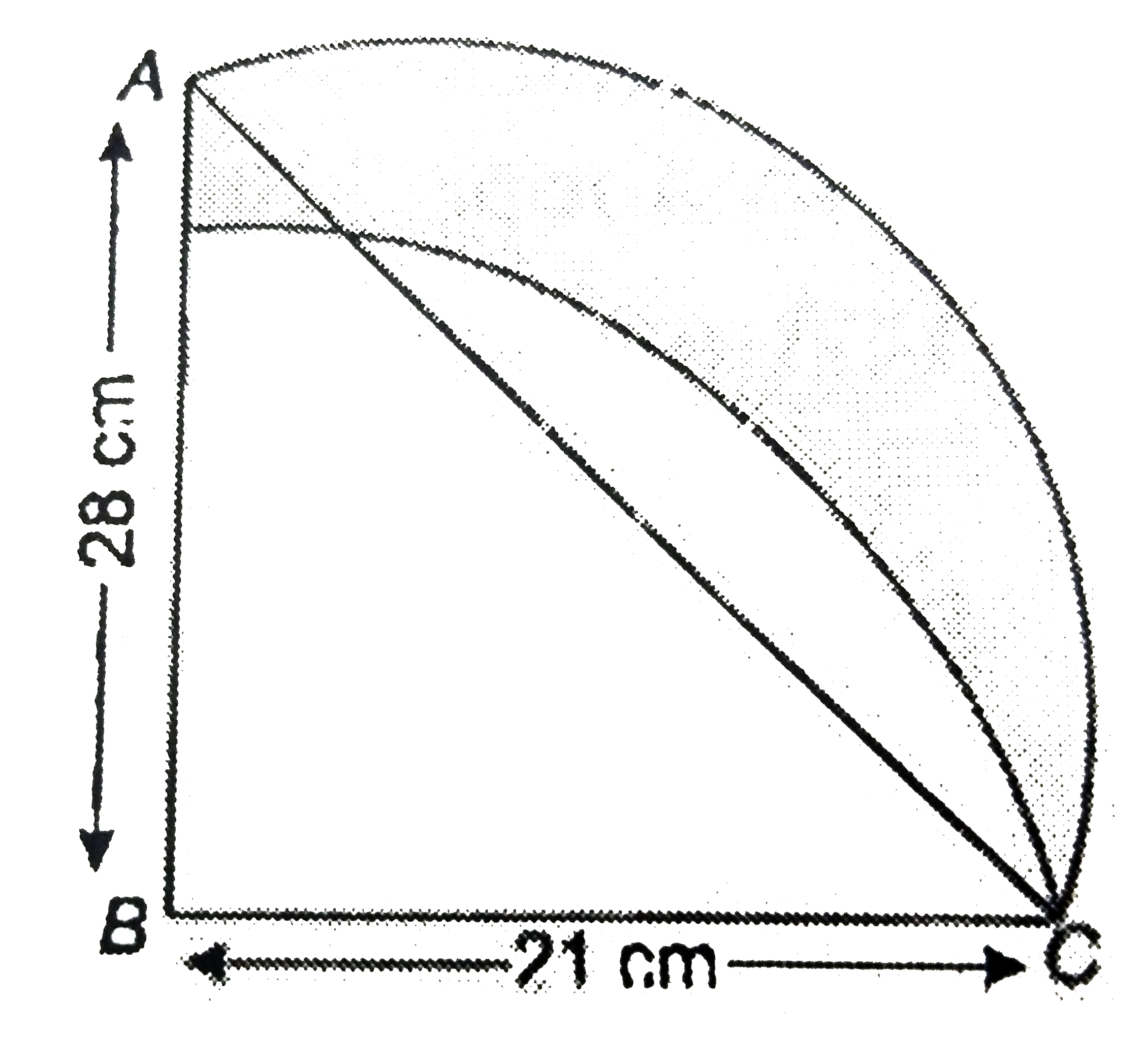 View Solution
View SolutionIn a right triangle ABC, ∠B=90∘
(a) If AB=6cm,BC=8cm, find AC
(b) If AC=13cm,BC=5cm, find AB.View Solution

