AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the length of radius AC
Step by step video & image solution for AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find the length of radius AC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABook:ICSEChapter:SECTION AND MID-POINT FORMULAExercise:QUESTIONS
Explore 17 Videos
- SECTION AND MID-POINT FORMULABook:ICSEChapter:SECTION AND MID-POINT FORMULAExercise:EXERCISE 13 (B)
Explore 20 Videos
- SAMPLE PAPER 5 (MATHEMATICS)Book:ICSEChapter:SAMPLE PAPER 5 (MATHEMATICS)Exercise:SECTION C
Explore 8 Videos
- SHARES AND DIVIDENDSBook:ICSEChapter:SHARES AND DIVIDENDSExercise:Exercise 3(C )
Explore 20 Videos
Similar Questions
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the coordinates of B.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionThe co-ordinates of the end points of a diameter of a circle are (3, -2) and (-3, 6). Find the co-ordinates of the centre and radius.
View SolutionIn the given figure AB is the diameter of a circle with centre O . If chord AC = chord AD, prove that :
(i) are BC=areDB
(ii) AB is bisector of ∠CAD.
Further, if the length of are AC is twice the length of are BC , find :
(i) ∠BAC
(ii) ∠ABC
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
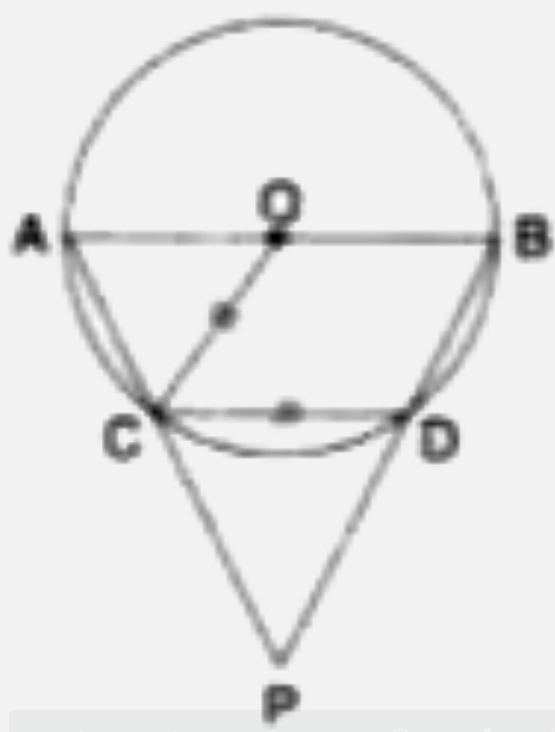
View SolutionOne end of a diameterof a circle is at (2,3) and the centre is (−2,5), find the coordinates of the other end of the diameter.
View SolutionThe end points of a diameter of a circle are (1,-1) and (3,5). Find the equation of the circle. Also find its centre and radius.
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
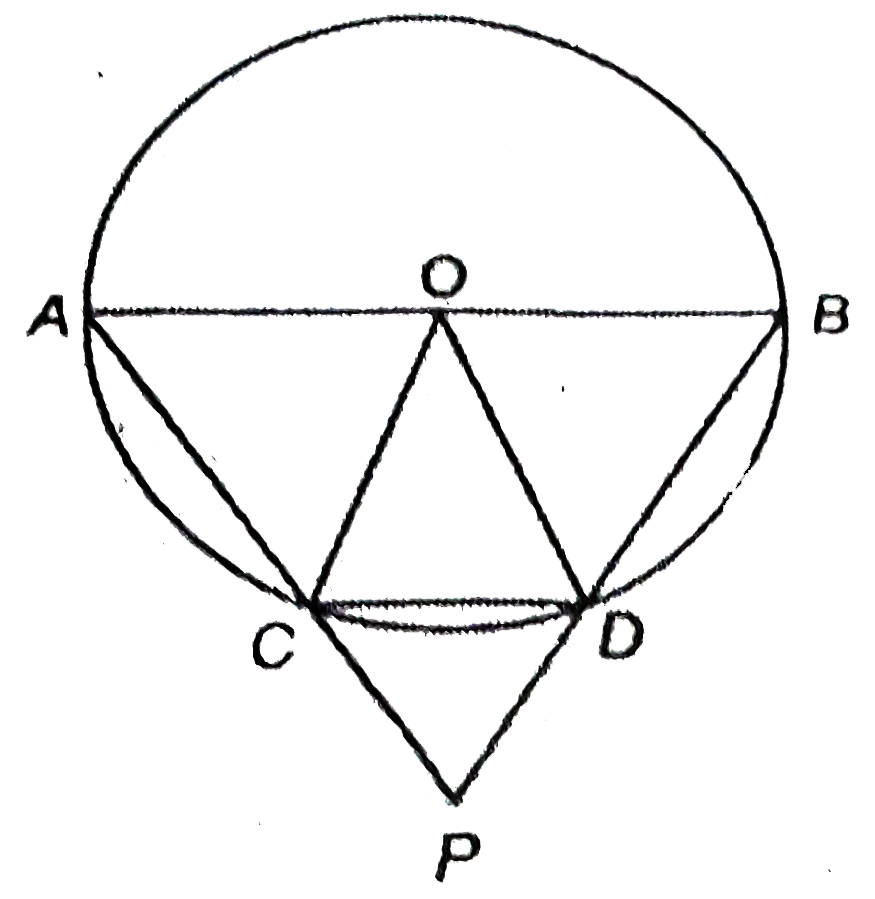
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View Solution
