The mid-point of the A segment AB, as shown in diagram, is C (4, -3). (4, -3) Write down the co ordinates of A and B.
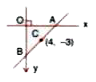
Step by step video & image solution for The mid-point of the A segment AB, as shown in diagram, is C (4, -3). (4, -3) Write down the co ordinates of A and B. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS17videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (B)20videos
SECTION AND MID-POINT FORMULA
- BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C8videos
SAMPLE PAPER 5 (MATHEMATICS)
- BOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )20videos
SHARES AND DIVIDENDS
Similar Questions
The mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
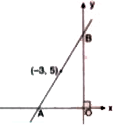. View SolutionP (-3, 2) is the mid point of line segment AB as shown in the given figure. Find the P (-3,2) co-ordinates of points A and B.
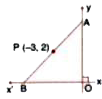
View SolutionThe point P (5,-4) divides the line segment AB, as shown in the figure, P (5, 4) in the ratio 2:5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
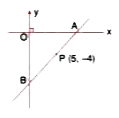
View SolutionIn the following diagram, write down :
the co-ordinates of the points A, B and C.View SolutionThe mid-point of the line segment joining (4a, 23) and (-4, 3b) is (2, -2a). Find the values of a and b
View SolutionUsing a graph paper, plot the points A (6, 4)and B(0, 4).
Write the co-ordinates of A' and B'.View SolutionIf (a,b) is the mid - point of the line segment joining the points A (10,-6), B(k,4) and a-2b =18, then find the value of k and the distance AB.
View SolutionIf the abscissa of a point P is 2, find the ratio in which this point divides the line segment joining the points (-4, 3) and (6,3). Also, find the co-ordinates of point P.
View SolutionThe point A(-3, 2) is reflected in the x-axis to the point A'. Point A' is then reflected in the origin to point A".
Write down the co-ordinates of A".View SolutionFind the position vector of the mid point of the line segment AB, where A is the point (3, 4, -2) and B is the point (1, ,2 4).
View Solution