In the figure, given alongside, ∠QPS=∠RPT
and ∠PRQ=∠PTS.

Prove that triangles PQR and PST are similar.
Step by step video & image solution for In the figure, given alongside, /_QPS = /_RPT and /_PRQ = /_PTS. Prove that triangles PQR and PST are similar. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(A)
48 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
In the figure, given alongside, ∠QPS=∠RPT
and ∠PRQ=∠PTS.

If PT : ST = 3:4, find the ratio between QR : PR.
View SolutionIn the given figure, AD = AE and AD2=BD×EC.
Prove that : triangles ABD and CAE are similar.
View SolutionIn the figure given alongside.
Name the adjacent angles.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
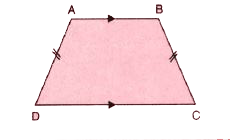
∠C=∠D
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
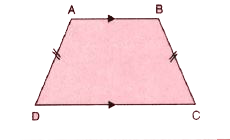
∠A=∠B
View SolutionIn Figure PSSQ=PTTRand ∠PST=∠PRQ. Prove that PQR is an isosceles triangle.
View SolutionIn the given figure, ∠PQR=∠PST=90∘, PQ = 5cm and PS = 2 cm.
Prove that △PQR ~△PST

View SolutionIn the figure, given below, straight lines AB and CD intersect at P, and AC//BD. Prove that :

ΔAPCandΔBPD are similar.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
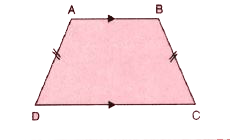
Diagonal AC= diagonal BD
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
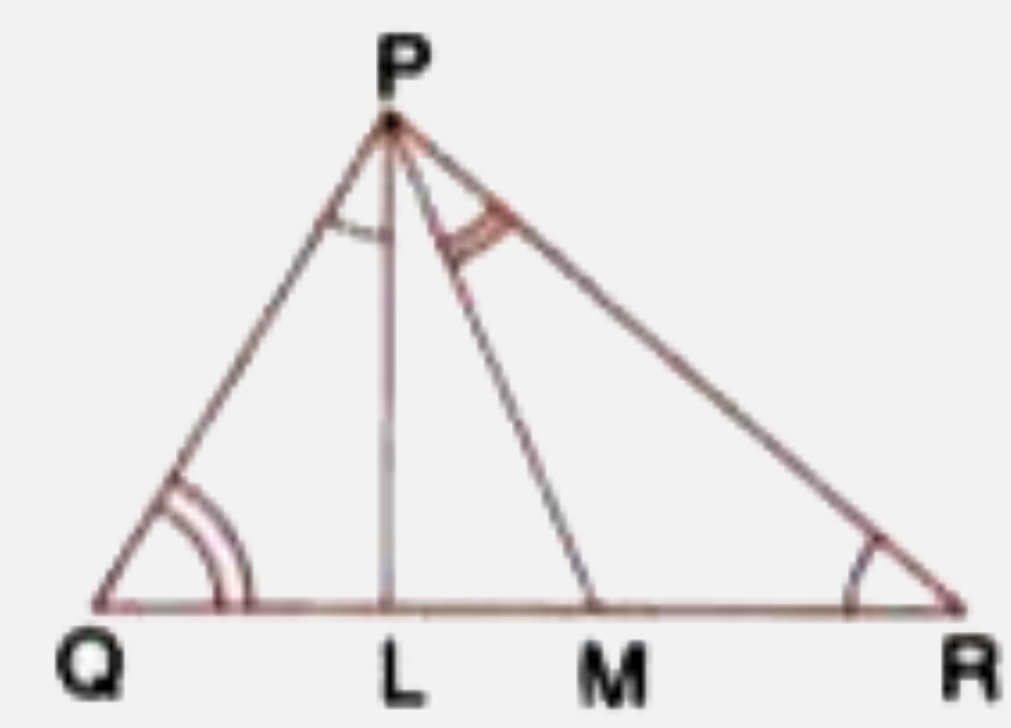
ΔPQL~ΔRPM
View Solution
