In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :

EF=FB
Step by step video & image solution for In the following figure, AD and CE are medians of DeltaABC. DF is drawn parallel to CE. Prove that : EF = FB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(D)
Explore 18 Videos
- SIMILARITY Book:ICSEChapter:SIMILARITY Exercise:MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
Explore 10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Book:ICSEChapter:SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Exercise:Exercise 6(e )
Explore 18 Videos
Similar Questions
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
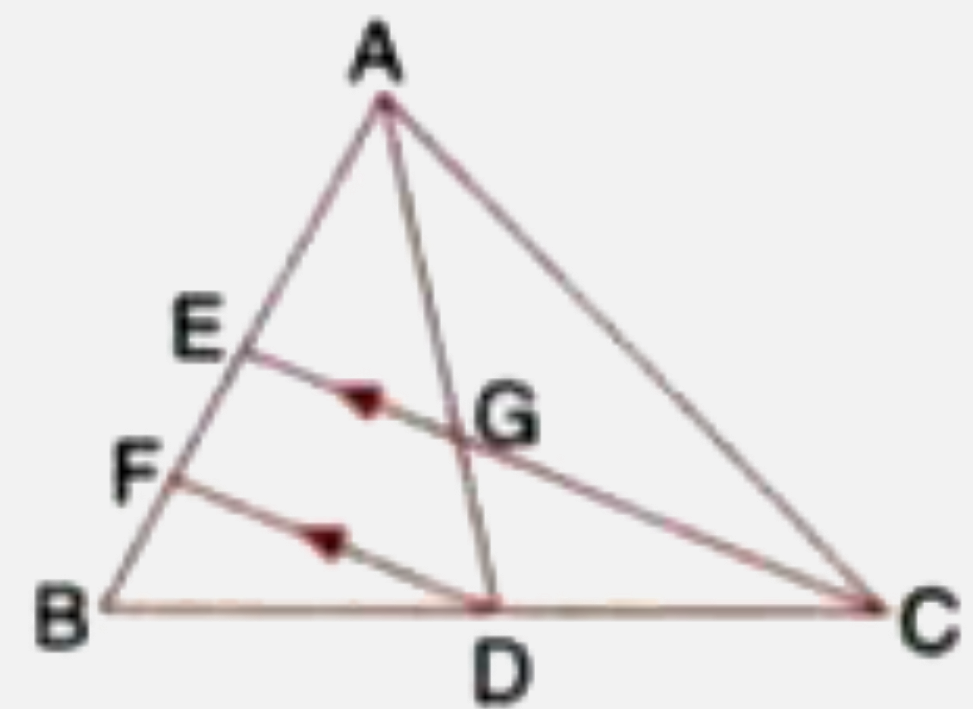
AG:GD=2:1.
View SolutionIn the following figure, if AD=DE. Prove that :
AB+BC>CE
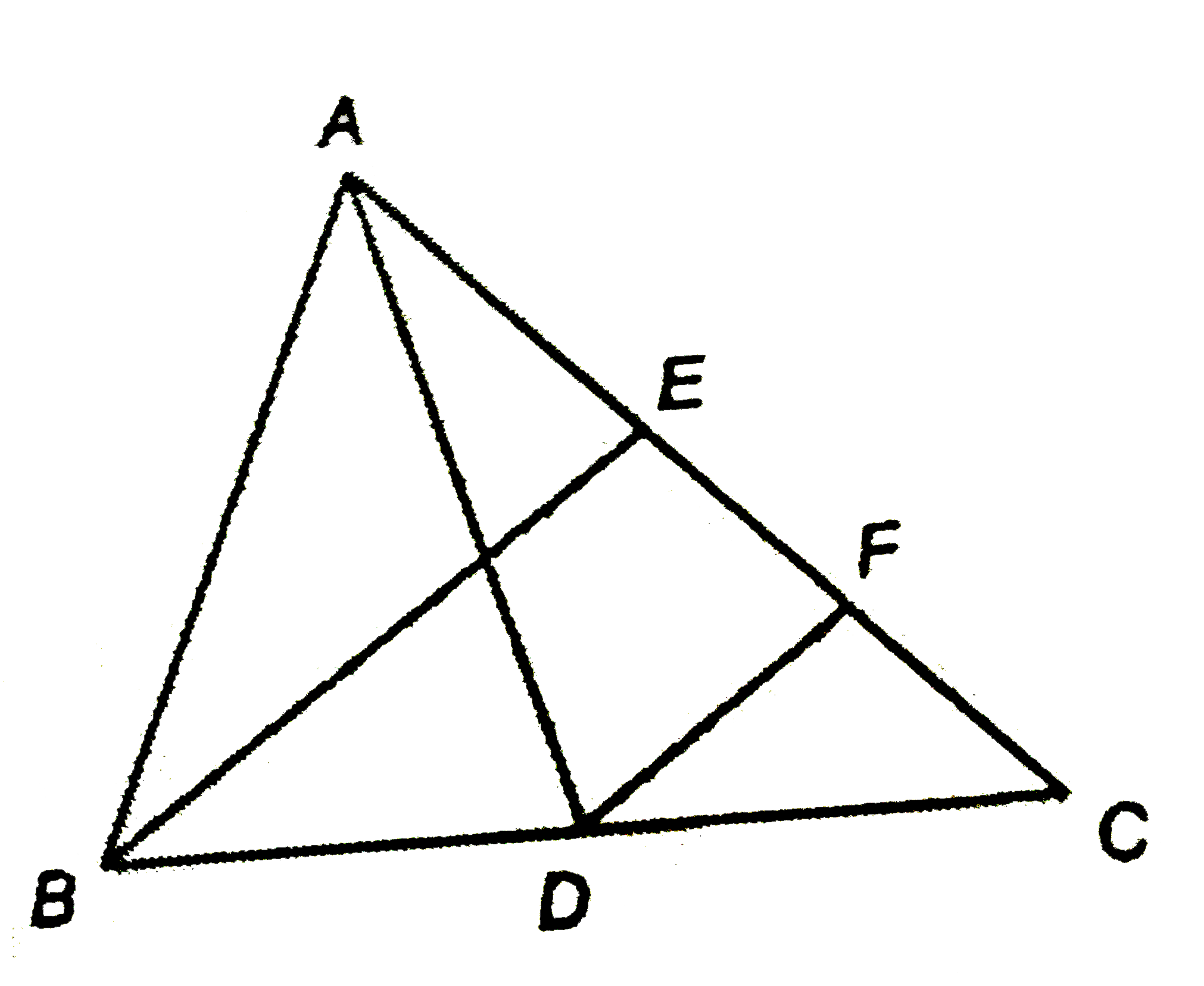
View SolutionIn the adjoining figure. AD and BE are two medians of ΔABC. IfDF||BE,then prove thatCF=14AC.
View SolutionIn the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
View SolutionIn the following figure, BL=CM
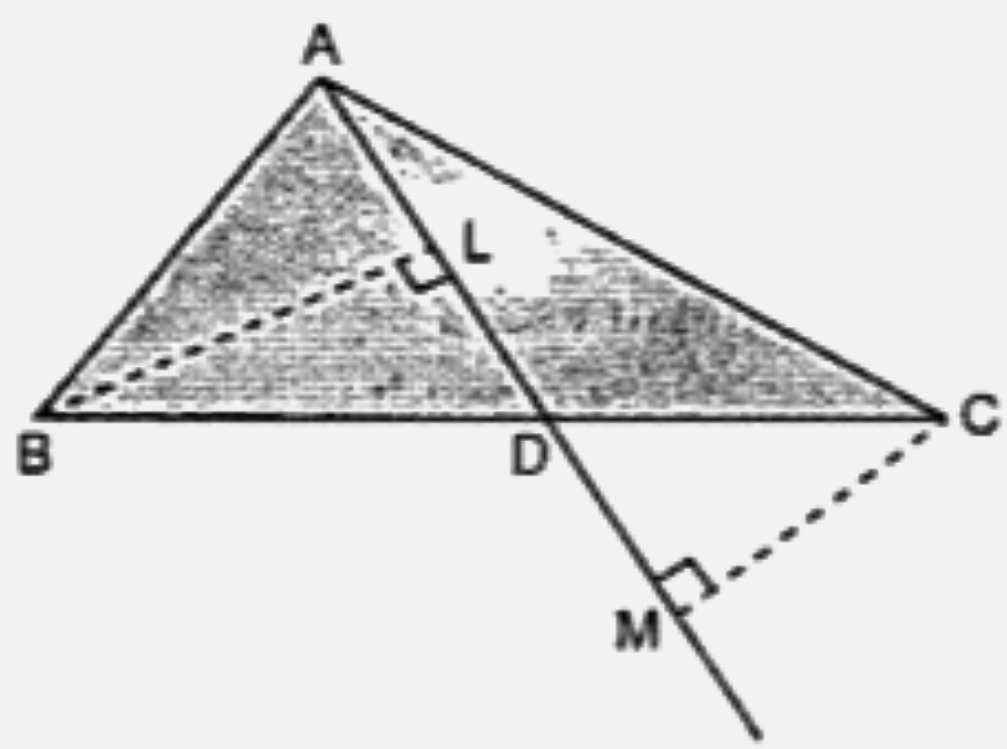
Prove that AD is a Median of triangle ABC
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
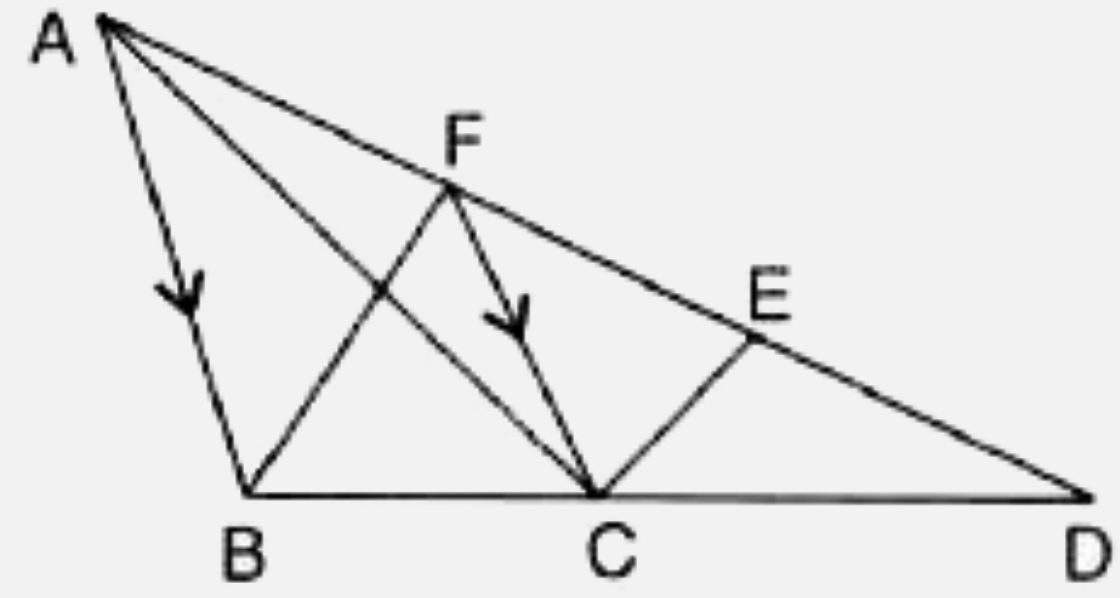
View SolutionIn the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
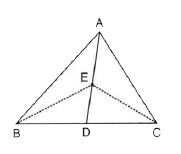
View SolutionIn the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
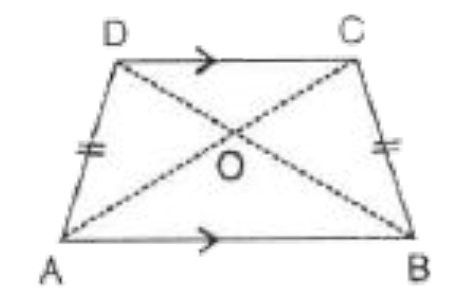
Prove that:
OA = OB and OC= OD
View Solution