The weights (in kilogram) of 5 persons are 67, 65, 71, 57 and 45. Find the arithmetic mean of their weights.
The correct Answer is:61 kg
To find the arithmetic mean of the weights of the 5 persons, we will follow these steps:
Step 1: List the weights
The weights of the 5 persons are:
- 67 kg
- 65 kg
- 71 kg
- 57 kg
- 45 kg
Step 2: Calculate the sum of the weights
Now, we will add all the weights together:
67+65+71+57+45
Calculating this step-by-step:
- First, add 67 and 65:
67+65=132
- Next, add 71:
132+71=203
- Then, add 57:
203+57=260
- Finally, add 45:
260+45=305
So, the total sum of the weights is 305 kg.
Step 3: Count the number of observations
The number of persons (observations) is 5.
Step 4: Calculate the arithmetic mean
Now we will use the formula for arithmetic mean:
Mean=Sum of all observationsTotal number of observations
Substituting the values we found:
Mean=3055
Step 5: Perform the division
Now, we divide 305 by 5:
- 5 goes into 30 six times (5 x 6 = 30), leaving a remainder of 0.
- Bring down the 5, and 5 goes into 5 one time (5 x 1 = 5).
So,
305÷5=61
Final Answer
The arithmetic mean of their weights is 61 kg.
---
The weights of the 5 persons are:
- 67 kg
- 65 kg
- 71 kg
- 57 kg
- 45 kg
Now, we will add all the weights together:
67+65+71+57+45
- First, add 67 and 65:
67+65=132
- Next, add 71:
132+71=203
- Then, add 57:
203+57=260
- Finally, add 45:
260+45=305
The number of persons (observations) is 5.
Now we will use the formula for arithmetic mean:
Mean=Sum of all observationsTotal number of observations
Substituting the values we found:
Mean=3055
Now, we divide 305 by 5:
- 5 goes into 30 six times (5 x 6 = 30), leaving a remainder of 0.
- Bring down the 5, and 5 goes into 5 one time (5 x 1 = 5).
305÷5=61
The arithmetic mean of their weights is 61 kg.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (A)17videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (B)10videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D25videos
MATRICES
- BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B52videos
MIXED PRACTICE
Similar Questions
Find the arithmetic mean of 4 and 12.
View SolutionFind the arithmetic mean between 5 and 9.
View SolutionFind 4 arithmetic means between -5 and 15.
View SolutionThe weights (in kg) of 50 wrestlers are recorded in the following table.

Find the mean weight of the wrestlers.View SolutionThe mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
View SolutionThe mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
View SolutionThe mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 53, 56 and 54. Find the weight of the seventh student.
View Solution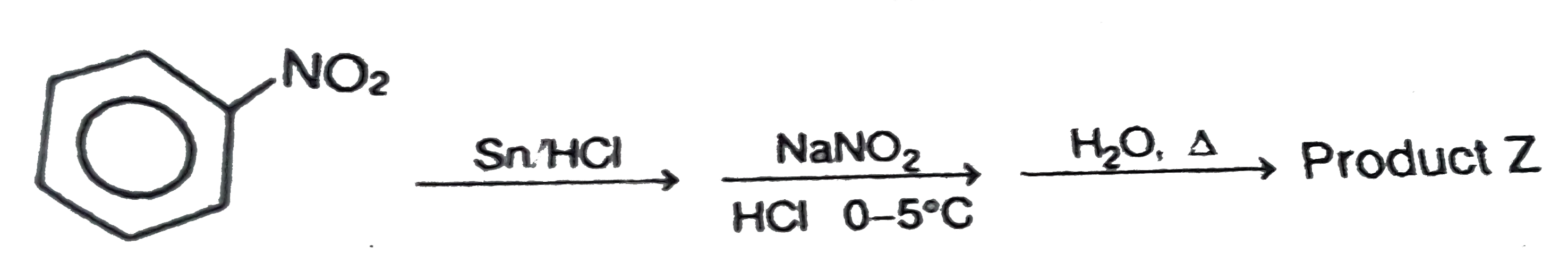
Find the molecular weight of Z.View Solution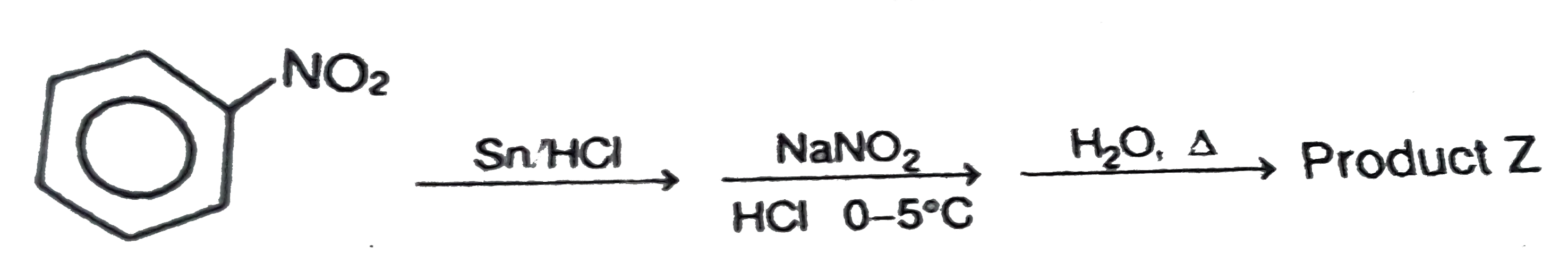
Find the molecular weight of Z.View SolutionMarks obtained (in mathematics) by 9 students are given below: 60, 67, 52, 76, 50, 51, 74, 45 and 56
a. Find the arithmetic mean.
b. If marks of each student be increased by 4, what will be the new value of arithmetic mean?View Solution

