The weights of 60 boys are given in the following distribution table:Find
(i) Median (ii) Lower quartile (iii) Upper quartile (iv) Inter quartile range
The correct Answer is:(i) 39 (ii) 38 (iii) 40 (iv) 2
To solve the problem step by step, we will follow the outlined process to find the median, lower quartile, upper quartile, and interquartile range for the weights of 60 boys given in a distribution table.
Step 1: Create the Cumulative Frequency (CF) Table
1. Find the Cumulative Frequency (CF):
- Start with the first frequency and keep adding the subsequent frequencies.
- For example, if the frequency distribution is as follows:
WeightRan≥|Frequency30−35|1035−40|1440−45|1845−50|1250−55|6
- The CF would be calculated as:
- CF for 30-35: 10
- CF for 35-40: 10 + 14 = 24
- CF for 40-45: 24 + 18 = 42
- CF for 45-50: 42 + 12 = 54
- CF for 50-55: 54 + 6 = 60
Step 2: Find the Median
2. Calculate the Median:
- The total number of observations (n) is 60, which is even.
- Use the formula for the median:
\(
\text{Median} = \frac{(n/2)^{th} + ((n/2) + 1)^{th}}{2}
\)
- Here, \( n/2 = 30 \) and \( (n/2) + 1 = 31 \).
- Find the 30th and 31st observations from the CF:
- The CF shows that the 30th observation falls in the class where CF is 42 (which corresponds to the weight range 40-45).
- The corresponding weight for the 30th observation is 39.
- Therefore, the median is:
\(
\text{Median} = 39
\)
Step 3: Find the Lower Quartile (Q1)
3. Calculate the Lower Quartile (Q1):
- The lower quartile is the 1st quartile, which is \( n/4 \).
- For \( n = 60 \), \( n/4 = 15 \).
- Check the CF to find the 15th observation:
- The CF shows that the 15th observation falls in the class where CF is 24 (which corresponds to the weight range 35-40).
- The corresponding weight for the 15th observation is 38.
- Therefore, the lower quartile (Q1) is:
\(
Q1 = 38
\)
Step 4: Find the Upper Quartile (Q3)
4. Calculate the Upper Quartile (Q3):
- The upper quartile is the 3rd quartile, which is \( 3n/4 \).
- For \( n = 60 \), \( 3n/4 = 45 \).
- Check the CF to find the 45th observation:
- The CF shows that the 45th observation falls in the class where CF is 54 (which corresponds to the weight range 45-50).
- The corresponding weight for the 45th observation is 40.
- Therefore, the upper quartile (Q3) is:
\(
Q3 = 40
\)
Step 5: Calculate the Interquartile Range (IQR)
5. Calculate the Interquartile Range (IQR):
- The interquartile range is calculated as:
\(
\text{IQR} = Q3 - Q1
\)
- Substituting the values:
\(
\text{IQR} = 40 - 38 = 2
\)
Final Answers:
- Median: 39
- Lower Quartile (Q1): 38
- Upper Quartile (Q3): 40
- Interquartile Range (IQR): 2
1. Find the Cumulative Frequency (CF):
- Start with the first frequency and keep adding the subsequent frequencies.
- For example, if the frequency distribution is as follows:
WeightRan≥|Frequency30−35|1035−40|1440−45|1845−50|1250−55|6
- The CF would be calculated as:
- CF for 30-35: 10
- CF for 35-40: 10 + 14 = 24
- CF for 40-45: 24 + 18 = 42
- CF for 45-50: 42 + 12 = 54
- CF for 50-55: 54 + 6 = 60
2. Calculate the Median:
- The total number of observations (n) is 60, which is even.
- Use the formula for the median:
\(
\text{Median} = \frac{(n/2)^{th} + ((n/2) + 1)^{th}}{2}
\)
- Here, \( n/2 = 30 \) and \( (n/2) + 1 = 31 \).
- Find the 30th and 31st observations from the CF:
- The CF shows that the 30th observation falls in the class where CF is 42 (which corresponds to the weight range 40-45).
- The corresponding weight for the 30th observation is 39.
- Therefore, the median is:
\(
\text{Median} = 39
\)
3. Calculate the Lower Quartile (Q1):
- The lower quartile is the 1st quartile, which is \( n/4 \).
- For \( n = 60 \), \( n/4 = 15 \).
- Check the CF to find the 15th observation:
- The CF shows that the 15th observation falls in the class where CF is 24 (which corresponds to the weight range 35-40).
- The corresponding weight for the 15th observation is 38.
- Therefore, the lower quartile (Q1) is:
\(
Q1 = 38
\)
4. Calculate the Upper Quartile (Q3):
- The upper quartile is the 3rd quartile, which is \( 3n/4 \).
- For \( n = 60 \), \( 3n/4 = 45 \).
- Check the CF to find the 45th observation:
- The CF shows that the 45th observation falls in the class where CF is 54 (which corresponds to the weight range 45-50).
- The corresponding weight for the 45th observation is 40.
- Therefore, the upper quartile (Q3) is:
\(
Q3 = 40
\)
5. Calculate the Interquartile Range (IQR):
- The interquartile range is calculated as:
\(
\text{IQR} = Q3 - Q1
\)
- Substituting the values:
\(
\text{IQR} = 40 - 38 = 2
\)
- Median: 39
- Lower Quartile (Q1): 38
- Upper Quartile (Q3): 40
- Interquartile Range (IQR): 2
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)8videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (E)23videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (B)10videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D25videos
MATRICES
- BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B52videos
MIXED PRACTICE
Similar Questions
From the following frequency distribution table find
(i) Lower quartile (ii) Upper quartile (iii) Inter quartile range
 View Solution
View SolutionThe marks obtained by 19 students of a class are given below:
27,36,22,31,25,26,33,24,37,32,29,28,36,35,27,26,32,35 and 28. Find
(i) Median (ii) Lower quartile
(iii) Upper quartile (iv) Inter quartile rangeView Solution
Knowledge Check
- Question 1 - Select One
For the data given the inter-quartile range is
A7B19C14D9
From the following data: find
(i) Median (ii) Upper quartile (iii) Inter quartile range:
25, 10,40,88,45,60,77,36,18,95,56,65,7,0,38 and 83View SolutionFind the lower quartile, upper quartile and inter quartile range for the date: 9,11,15,19,17,13,7
View SolutionThe weights in kilograms of 60 workers in a factory are given in the following frequency table. Find the mean weight of a worker. Weight (in kg) x: 60 61 62 63 64 65 No. of workers f: 5 8 14 16 10 7
View SolutionA random variable X has the following probability distribution:
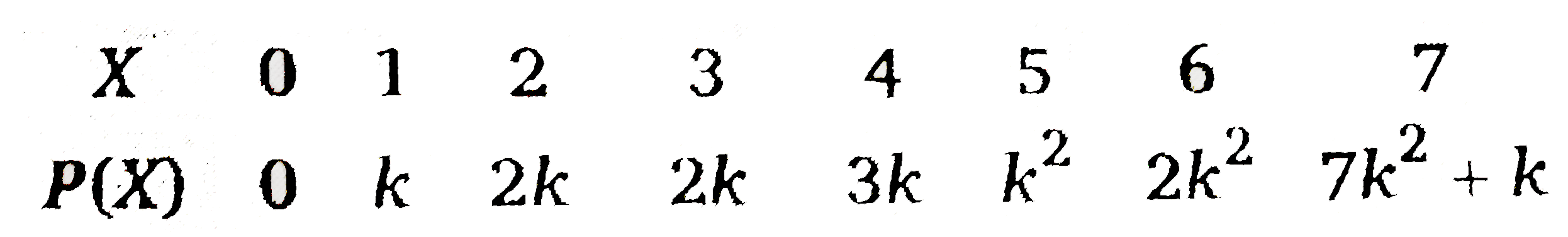
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)View SolutionDefine the following terms: (i)Observations (ii) data (iii) Frequency of an observation (iv) Frequency distribution
View SolutionDefine the following terms: (i) Observations (ii) data (iii) Frequency of an observation (iv)Frequency distribution
View SolutionThe table shows the distribution of the scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution. (Take 2 cm = 10 scores on the X-axis and 2 cm = 20 shooters on the Y-axis)

Use your graph to estimate the following :
(i) The median.
(ii) The interquartile range.
(iii) The number of shooters who obtained a score of more than 85%.View Solution

