DEF is the triangle formed by joining the points of contact of the incircle with the sides of the triangle ABC, prove that its sides are 2rcosA2, 2rcosB2 and 2rcosC2 where r is the radius of incircle of ABC. its angles are π2−A2,π2−B2andπ2−C2 its area is r2s2R where 's' is the semiperimter and R is the circumradius of the ABC .
To prove the properties of triangle DEF formed by joining the points of contact of the incircle with the sides of triangle ABC, we will follow these steps:
Step 1: Understanding the Triangle DEF
The triangle DEF is known as the contact triangle or intouch triangle of triangle ABC. The points D,E,F are the points where the incircle touches the sides BC,CA, and AB respectively.
Hint: Recall that the points of tangency of the incircle with the sides of a triangle are significant in defining the contact triangle.
Step 2: Finding the Sides of Triangle DEF
The sides of triangle DEF can be expressed in terms of the angles of triangle ABC and the radius r of the incircle. The lengths of the sides DE,EF, and FD can be derived as follows:
- DE=2rcos(A2)
- EF=2rcos(B2)
- FD=2rcos(C2)
Hint: Use the relationship between the sides of the triangle and the angles to derive the expressions for the sides of triangle DEF.
Step 3: Finding the Angles of Triangle DEF
The angles of triangle DEF can be calculated using the angles of triangle ABC:
- ∠D=π2−A2
- ∠E=π2−B2
- ∠F=π2−C2
Hint: The angles of the contact triangle are complementary to half of the angles of the original triangle ABC.
Step 4: Finding the Area of Triangle DEF
The area A of triangle DEF can be expressed in terms of the radius r of the incircle, the semiperimeter s of triangle ABC, and the circumradius R of triangle ABC:
Area=r2s2R
Hint: Use the formula for the area of a triangle in terms of its incircle radius and circumradius.
Conclusion
We have shown that:
1. The sides of triangle DEF are 2rcos(A2),2rcos(B2),2rcos(C2).
2. The angles of triangle DEF are π2−A2,π2−B2,π2−C2.
3. The area of triangle DEF is r2s2R.
The triangle DEF is known as the contact triangle or intouch triangle of triangle ABC. The points D,E,F are the points where the incircle touches the sides BC,CA, and AB respectively.
The sides of triangle DEF can be expressed in terms of the angles of triangle ABC and the radius r of the incircle. The lengths of the sides DE,EF, and FD can be derived as follows:
- EF=2rcos(B2)
- FD=2rcos(C2)
The angles of triangle DEF can be calculated using the angles of triangle ABC:
- ∠E=π2−B2
- ∠F=π2−C2
The area A of triangle DEF can be expressed in terms of the radius r of the incircle, the semiperimeter s of triangle ABC, and the circumradius R of triangle ABC:
We have shown that:
1. The sides of triangle DEF are 2rcos(A2),2rcos(B2),2rcos(C2).
2. The angles of triangle DEF are π2−A2,π2−B2,π2−C2.
3. The area of triangle DEF is r2s2R.
Topper's Solved these Questions
Similar Questions
In a triangle ABC, prove that the ratio of the area of the incircle to that of the triangle is π:cot(A2)cot(B2)cot(C2)
View SolutionIf a,b and c are sides of a ritht triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r=a+b−c2.
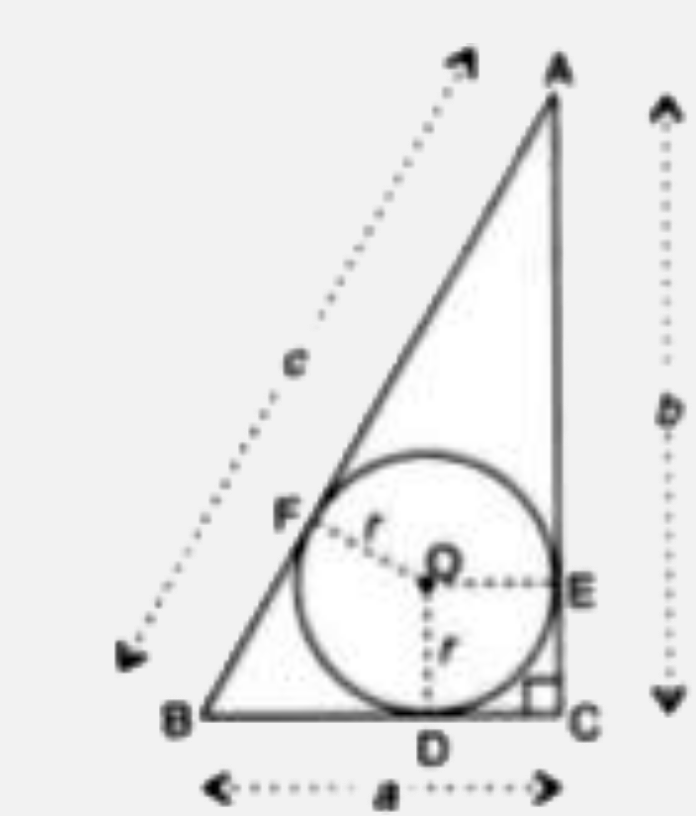
View SolutionIf a,b,c are the sides of a right triangle , where c is the hypotenuse. Prove that the radius r of the circle which touches the sides of the triangle is given by:r=a+b−c2
View SolutionIn a triangle ABC, 8R2=a2+b2+c2 prove that the triangle is right angled
View SolutionProve that a2+b2+c2+2abc<2, where a,b,c are the sides of triangle ABC such that a+b+c=2.
View SolutionIn triangle ABC, let ∠C=π/2. If r is the inradius and R is circumradius of the triangle, then 2(r+R) is equal to
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2 .
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2.
View SolutionIn a triangle ABC, prove that r2+r21+r22+r23=16R2−a2−b2−c2.
View SolutionIf in a triangle ABC, the altitude AM be the bisector of ∠BAD,whereD is the mid point of side BC , then prove that (b2−c2)=a2/2.
View Solution
