In the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
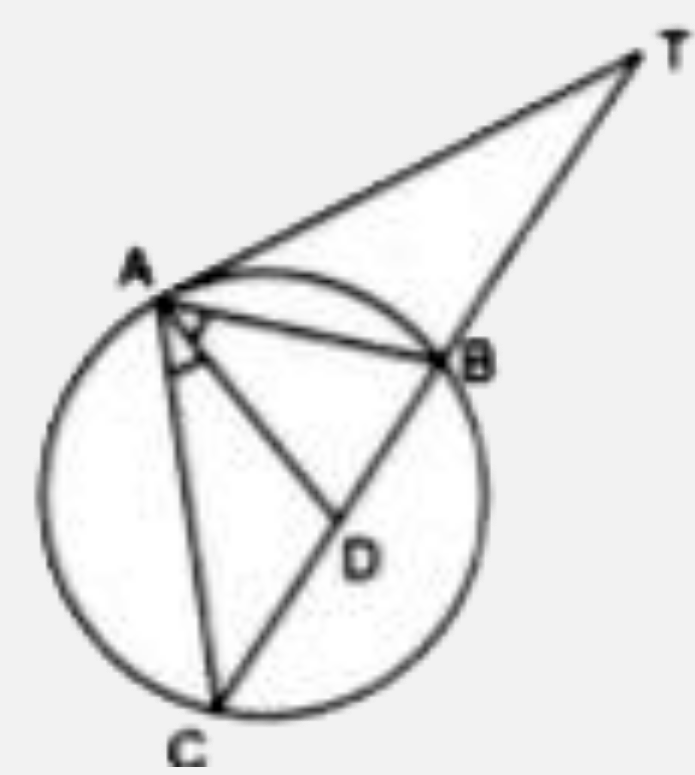
Step by step video & image solution for In the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that: Delta ADT is isosceles. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
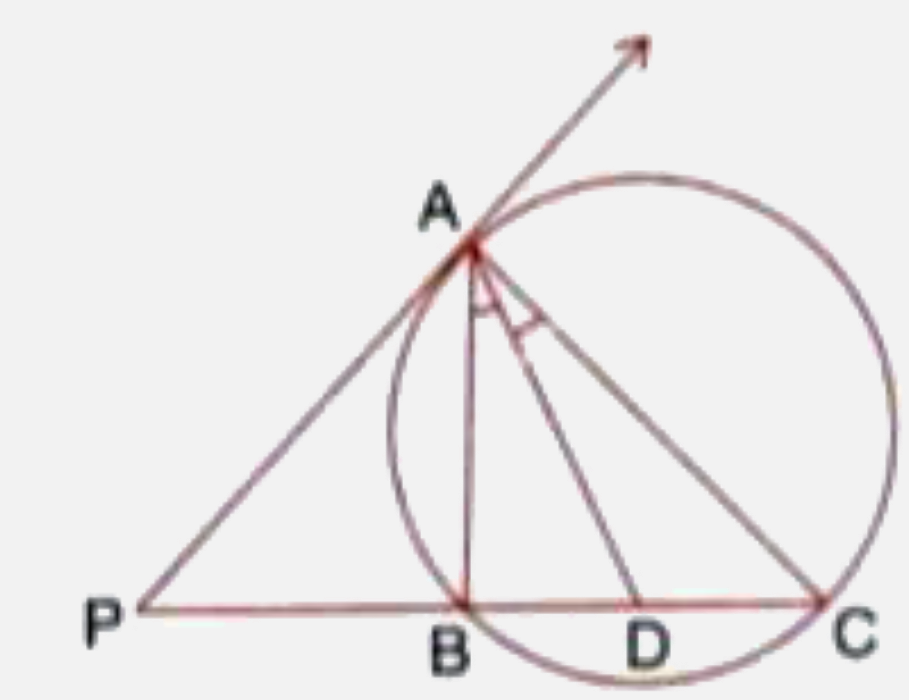
∠CAD=12[∠PBA−∠PAB]
View SolutionIn a fig. PA is a tangent to the circle. PBC is a secant & AD bisects angle BAC. Show that triangle PAD is an isosceles triangle.Also show that ∠CAD=12(∠PBA−∠PAB)
View SolutionIn a triangle ABC, side AC is greater than side AB and point D lies on side BC such that AD bisects angle BAC. Show that:
∠ADB is acute.
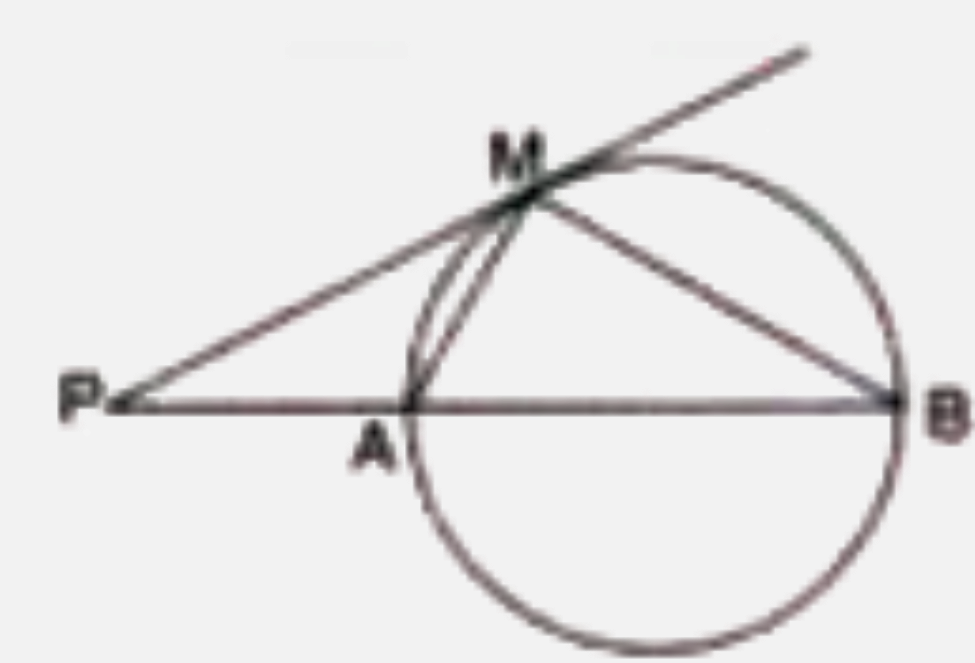
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
View SolutionABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
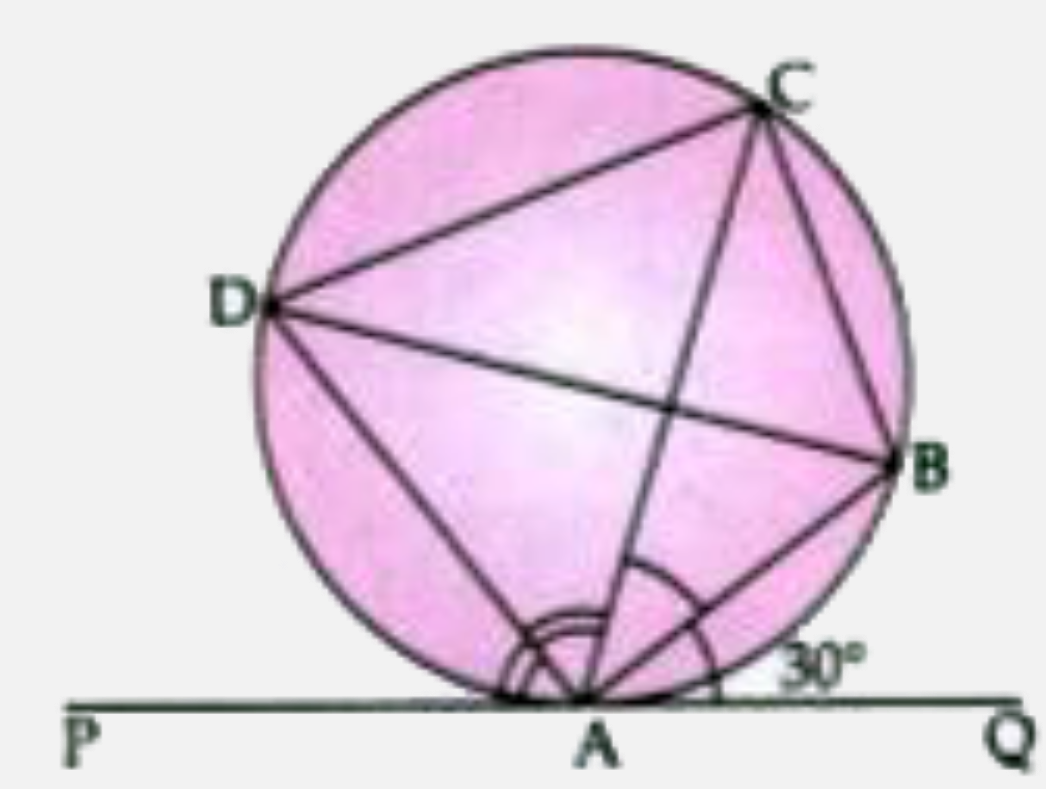
View SolutionIn the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQand∠PAC. If ∠BAQ=30∘, prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
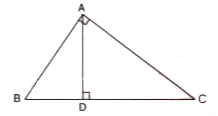
Prove that : ΔABD is similar to ΔCAD.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionP is a point on the bisector of ∠ABC .If the line through P, parallel to BA meet at Q ,prove that ΔBPQ is an isosceles triangle.
View Solution
