ABCD is a parallelogram and P is a point of ¯¯¯¯¯¯CD. Show that ar(△ABP) = ar(△ADP+△BCP).Solution in Telugu
Step by step video & image solution for ABCD is a parallelogram and P is a point of bar(CD). Show that ar(/_\ABP) = ar(/_\ADP+ /_\BCP). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC is a triangle . D is a point of AB such that AD=14ABandE is a point on AC such that AE=14AC. If DE=2cm find BC.
View SolutionState which of the following are mathematical statements and which are not? Give reason.
She has blue rays
View SolutionSimplify the following expressions .
i) (5+√7)(2+√5)
ii) (5+√5)(5−√5)
iii) (√3+√7)2
iv) (√11−√7)(√11+√7)
View SolutionP और Q क्रमश : समांतर चतुर्भुज ABCD कि भुजाओ में DC और AD पर स्थित बिंदु है । दर्शाइए कि ar(APB)=ar(BQC) है |
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

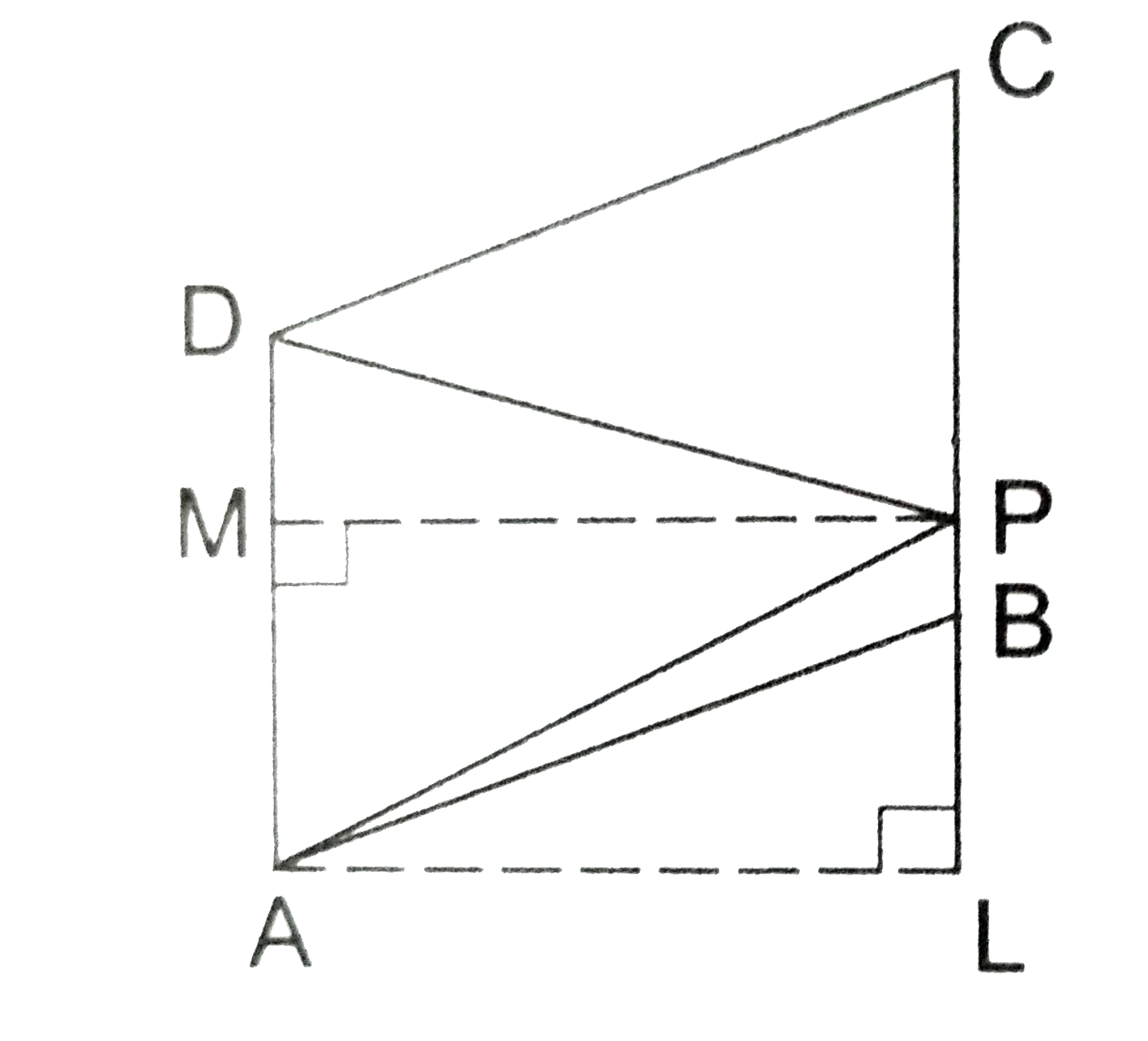
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View SolutionP और Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर बिन्दु है। दर्शाइए कि ar (APB) = ar (BQC) है।
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View SolutionP और Q किसी समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित दो बिंदु है |दिखाएँ की ar(ΔAPB)=ar(ΔBQC)
View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
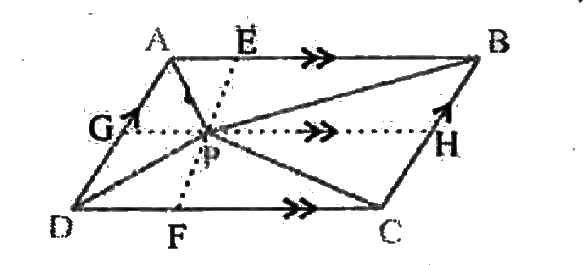
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionIn the given figure, ABED is a parallelogram and DE and EC . Prove that ar (ABF)=ar(BEC)

View SolutionIn figure, ABCD and EFGD are two parallelograms and G is the mid-point of side CD. Then, ar (DPC) = (1)/(2) ar(EFGD).
View SolutionABCD is a parallelogram and P is a point of ¯¯¯¯¯¯CD. Show that ar(△ABP) = ar(△ADP+△BCP).
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that (i) ar (triangleAPB)+ar(trianglePCD=1/2ar(ABCD) (ii) ar (triangleAPD)+ar(trianglePBC)=ar(triangleAPB)+ar(trianglePCD)
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that ar (APB) + ar (PCD) = 1/(2) ar (ABCD)
View Solution
