In the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
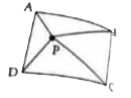
Step by step video & image solution for In the adjacent figure P is a point inside the parallelogram ABCD. Prove that ar (APB) + ar (PCD) = 1/(2) ar (ABCD) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERAL BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7A
31 Videos
- QUADRILATERAL BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B
6 Videos
- LINES AND ANGLES BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B
5 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B
10 Videos
Similar Questions
In the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
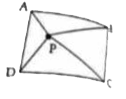
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
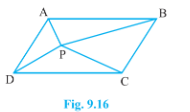
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
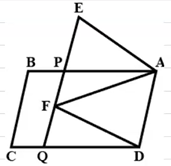
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionO is the any point on diagonal PR of parallelogram PQRS. Prove that Ar(PSO) = Ar(PQO)
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View Solution
