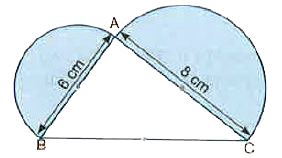
A triangle is drawn by joining a point on a semicircle to the end of the
diameter. Then semicircles are drawn with the other two sides as diameter.
'(##VPU_TTT_MAT_X_P01_C02_E01_009_Q01##)'
Prove that the sum of the areas of the blue and red crescents in the second pictúre is equai to the area of the triangle.Solution in Malayalam
Step by step video & image solution for A triangle is drawn by joining a point on a semicircle to the end of the diameter. Then semicircles are drawn with the other two sides as diameter. '(##VPU_TTT_MAT_X_P01_C02_E01_009_Q01##)' Prove that the sum of the areas of the blue and red crescents in the second pictúre is equai to the area of the triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
One cubic centimetre of iron weighs 7.8 grams. Write as sequences, the volumes of weights of Iron cubes of sides 1 centimetre, 2 centimetres and so on.
View SolutionFind the following:
i) The y coordinate of any point on the 'x' axis.
ii) The 'x' coordinate of any point on the 'y' axis.
iii) The coordinates of the origin.
iv) The y coordinate of any point on the line through (0,1), parallel to the 'x' axis.
v) The x coordinate of any point on the line through (1,0), parallel to the 'y' axis.
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionIn a Delta ABC, a semicircle is inscribed,whose diameter lies on the side c.Then the radius of the semicircle is (Where Delta is the area of the triangle ABC)
View SolutionIn a right -angle triangle, the length of the sides containing the right angles area aandb. With the mid-point of each sides as centres three semicircles are drawn outiside the triangle. Find the area of Δ and the semicircles together
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View Solutionangle A At right angles Delta ABC Assuming the side AC of the diameter to be drawn, a semicircle is drawn. If a chord connects the point and the intersection of the hypotenuse and the semicircle of the triangle, then the length of the side AC is
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View Solutionसिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए अर्धवृत्त का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए अर्धवृत्तों के क्षेत्रफलों के योग के बराबर होता है।
View Solutionकिसी त्रिभुज ABC में एक अर्द्धवृत्त अन्तर्गत है जिसका व्यास भुजा C पर स्थित है। तो अर्द्धवृत्त की त्रिन्या होगी (जहाँ △ त्रिभुज ABC का क्षेत्रफल है)
View Solutionसिद्ध कीजिए कि समकोण त्रिभुज के कर्ण पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल , अन्य दो भुजाओं पर बनाए गए समबाहु त्रिभुजों के क्षेत्रफलों का योग के बराबर होता है।
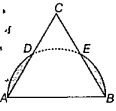
View SolutionThe diameter of a semicircle and the base of an equilateral △ABC coincide in such a way that the other two sides of the triangle intersect the circumference of the semicircle at the points D and E, as shown in the diagram. If the perimeter of the triangle ABC is 6 cm, find the area of the shaded region.
View SolutionABC एक समद्विबाहु समकोण त्रिभुज है तथा AC इसका कर्ण है। इसकी भुजा AC को लेकर एक वर्ग बनाया गया है जिसका क्षेत्रफल 128 वर्ग सेमी है तदनुसार भुजा AB तथा AC को व्यास लेकर खींचे गए अर्द्धवृत्तो के क्षेत्रफलों का योग क्या होगा ?
View SolutionProve that the area of the equilateral triangle drawn on the hypotenuse of a right angle triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides.
View Solution
