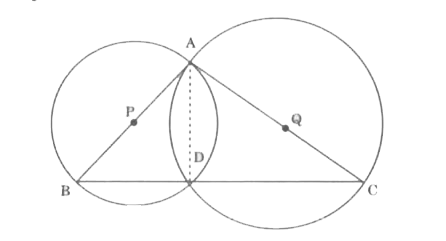
In the figure '/_ P=90^circ .' Sides of triangle APC are extended to 'B' and 'D'.
'(##VPU_TTT_MAT_X_P01_C02_E14_005_Q01##)'
a) If a circle is drawn with 'A C' as its diameter, where will be position of P with respect to that circle?
b) What about the position of 'P', if the circle is drawn with AD as diameter?
c) Prove that, the circles drawn with the sides of a qủadrilateral with perpendicular diagonals, will meet-at a common point.Solution in Malayalam
Step by step video & image solution for In the figure '/_ P=90^circ .' Sides of triangle APC are extended to 'B' and 'D'. '(##VPU_TTT_MAT_X_P01_C02_E14_005_Q01##)' a) If a circle is drawn with 'A C' as its diameter, where will be position of P with respect to that circle? b) What about the position of 'P', if the circle is drawn with AD as diameter? c) Prove that, the circles drawn with the sides of a qủadrilateral with perpendicular diagonals, will meet-at a common point. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
One cubic centimetre of iron weighs 7.8 grams. Write as sequences, the volumes of weights of Iron cubes of sides 1 centimetre, 2 centimetres and so on.
View SolutionFind the following:
i) The y coordinate of any point on the 'x' axis.
ii) The 'x' coordinate of any point on the 'y' axis.
iii) The coordinates of the origin.
iv) The y coordinate of any point on the line through (0,1), parallel to the 'x' axis.
v) The x coordinate of any point on the line through (1,0), parallel to the 'y' axis.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point ofintersection of these circles lie on the third side
View SolutionIf circles are drawn taking two sides of a triangle as diameters,prove that the pooint of intersection of these circles lie on the third side
View SolutionIn a right angle triangle with sides a,b,c,a circle is drawn inside is touching its sides to prove =(a+b-c)/(2)= radius of circle.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point ofintersection of these circles lie on the third side
View SolutionIn the side figure, the two tangents drawn from the outer point C to the circle with center O touch the points P and Q, respectively. The tangent CP and CQ drawn on another point R of the circle intersect at points A and B respectively. If, CP=11 Cm. And BC=7 Cm. If so, determine the length of the BR.
View SolutionIn a right-triangle ABC in which ∠B=90∘, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
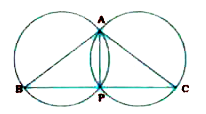
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A △ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D. To Prove: BD=DC Construction : Join AD.
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
View Solution
