In a right-triangle ABC in which ∠B=90∘, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.Solution in Kannada
Step by step video & image solution for In a right-triangle ABC in which angleB=90^(@), a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( LONG ANSWER [LA] TYPE - QUESTIONS)
8 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
2 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE 1 - QUESTIONS)
16 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ZEN ADDITIONAL QUESTIONS (HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
4 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS [HOTS] QUESTIONS
14 Videos
Similar Questions
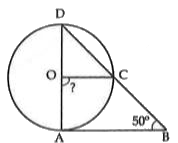
In the given figure, AD is a diameter of a circle with centre O and AB is a tangent at A. C is a point on the circle such that DC produced intersects the tangent at B and ⌊ABD=50∘. Find ⌊COA.
View SolutionIf a, b, and c, are the sides of a right-angled triangle where C is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r=a+b−c2 units.
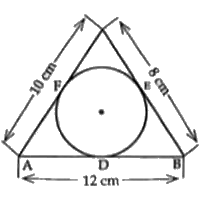
View SolutionIn the given figure, a circle is inscribed in a ΔABC such that it touches the sides AB, BC, and CA at points D, E, and F respectively. If the lengths of the sides AB, BC, and CA are 12 cm, 8 cm, and 10 cm respectively, find the lengths of AD, BE, and CF.
View SolutionIf m times the mth term of an A.P. is equal ton times the nth term and m≠n, show that (m+n)th term is zero.
View SolutionIn what ratio does 4x +3y-13 0 divide the line segment joining (2, 1) and (1, 4)?
View SolutionIn a right angle triangle Delta ABC is which /_B=90^(@) a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D To Prove: BD=DC Construction : Join AD
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionLet ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B=90∘ . BD is the= perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
View SolutionLet ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B=90∘. BD is the= perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
View Solutionसमकोण त्रिभुज ABC क़ि भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को P पर प्रतिच्छेद करता है सिद्ध कीजिये क़ि बिंदु P पर वृत्त क़ि स्पर्श रेखा भुजा BC को समद्विभाजित करती है।
View SolutionA right triangle is drawn at ABC with a circle of diameter AB denoting AC denoting P at P. Prove that the tangent drawn to a circle through P isosceles the BC shoulder.
View SolutionABC एक समकोण त्रिभुज है जिसमे ∠B=90∘ है। AC को व्यास मानकर खींचा गया वृत्त AB को बिन्दु D पर काटता है। निम्नलिखित में कौन-सा सत्य है?
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View Solution
