In a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.Solution in Bengali
Step by step video & image solution for In a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT BANGLISHCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Exercise (9.3)
8 Videos
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT BANGLISHCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Optional exercise
7 Videos
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT BANGLISHCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Exercise (9.1)
5 Videos
- STATISTICSBOOK - NCERT BANGLISHCHAPTER - STATISTICSEXERCISE - THINK AND DISCUSS
8 Videos
- TRIGONOMETRY BOOK - NCERT BANGLISHCHAPTER - TRIGONOMETRY EXERCISE - OPTIONAL EXERCISE
6 Videos
Similar Questions
Fill the blank: Atmost ______ tangent can drawn from any point on the circle.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionFill in the blanks
(i) A tangent to a circle touches it in …... Point (s).
(ii) A line intersecting a circle in two points is called a …..
(iii) Number of tangents can be drawn to a circle parallel to the given tangent is ….
(iv) The common point of a Tangent to a circle and the circle is called .....
(v) We can draw ..... tangents to a given circle.
(vi) A circle can have ..... parallel tangents at the most.
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View SolutionProve that cotθ−cosθcotθ+cosθ=cosecθ−1cosecθ+1
View SolutionTwo circles are drawn with sides AB and AC of a triangle ABC as diameters
View SolutionIn a right angle triangle Delta ABC is which /_B=90^(@) a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D To Prove: BD=DC Construction : Join AD
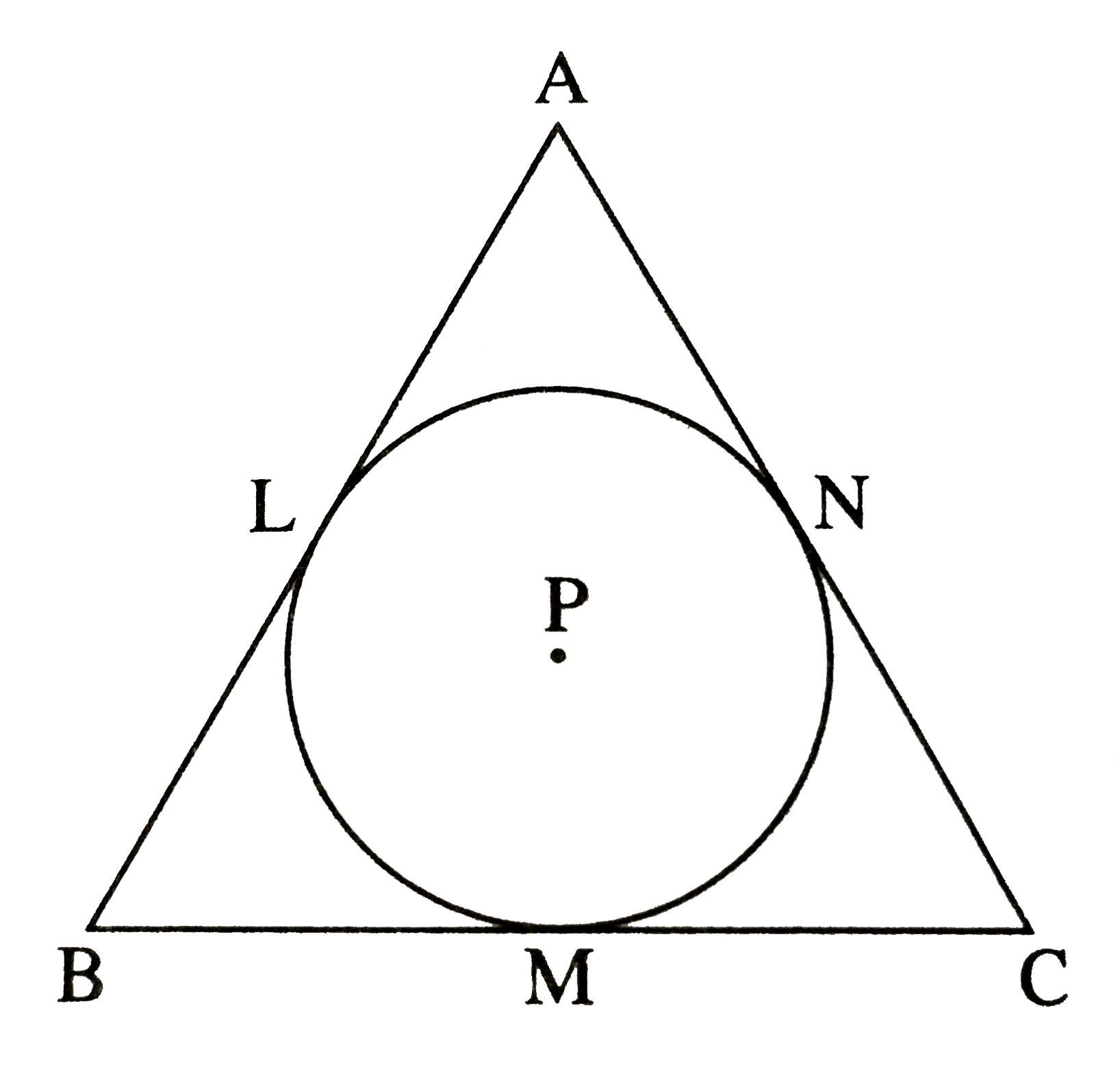
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
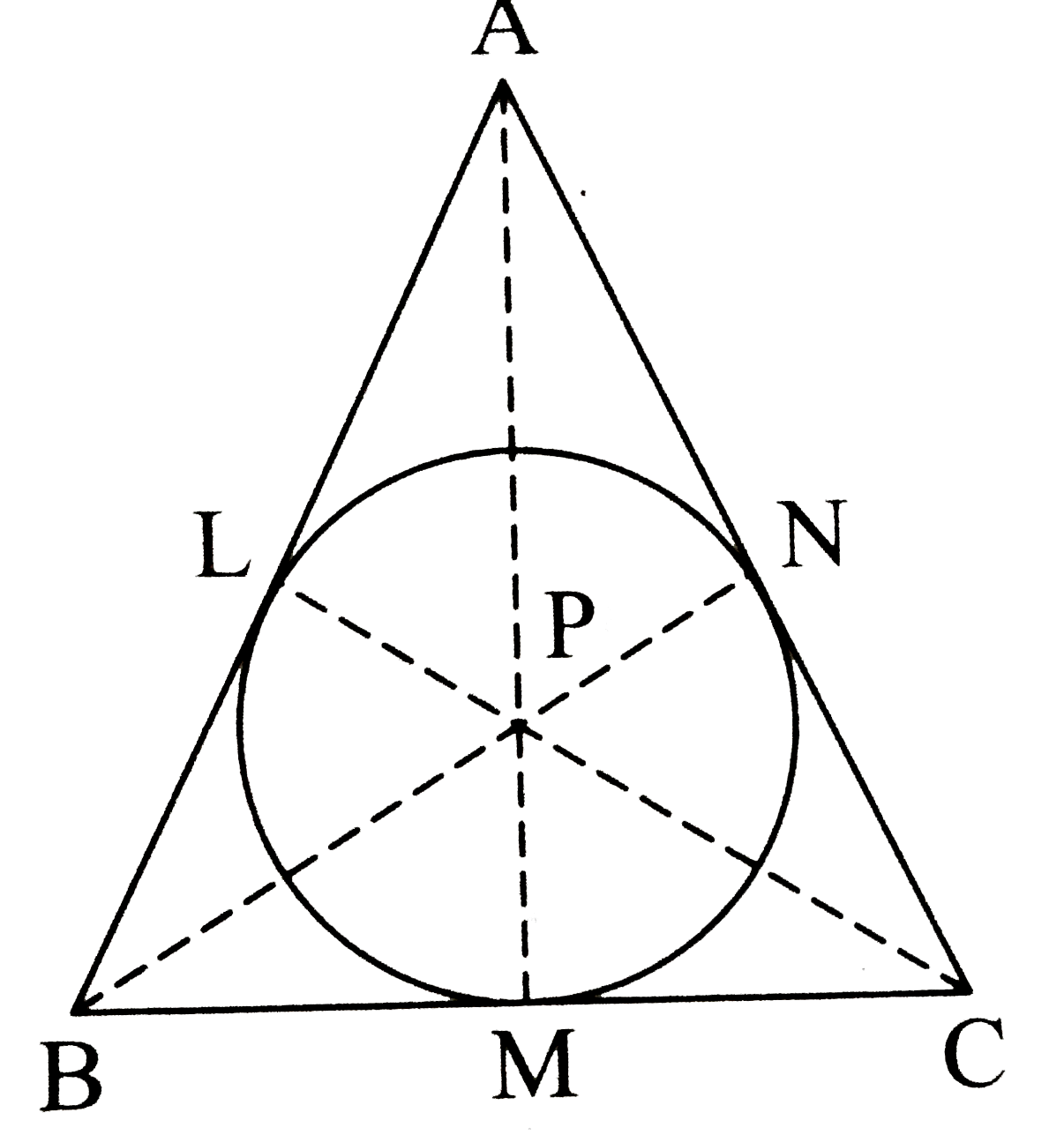
View SolutionA circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
View Solutionसमकोण त्रिभुज ABC क़ि भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को P पर प्रतिच्छेद करता है सिद्ध कीजिये क़ि बिंदु P पर वृत्त क़ि स्पर्श रेखा भुजा BC को समद्विभाजित करती है।
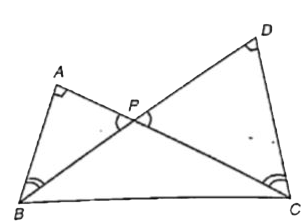
View SolutionTwo right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
View SolutionA right triangle is drawn at ABC with a circle of diameter AB denoting AC denoting P at P. Prove that the tangent drawn to a circle through P isosceles the BC shoulder.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View Solution
