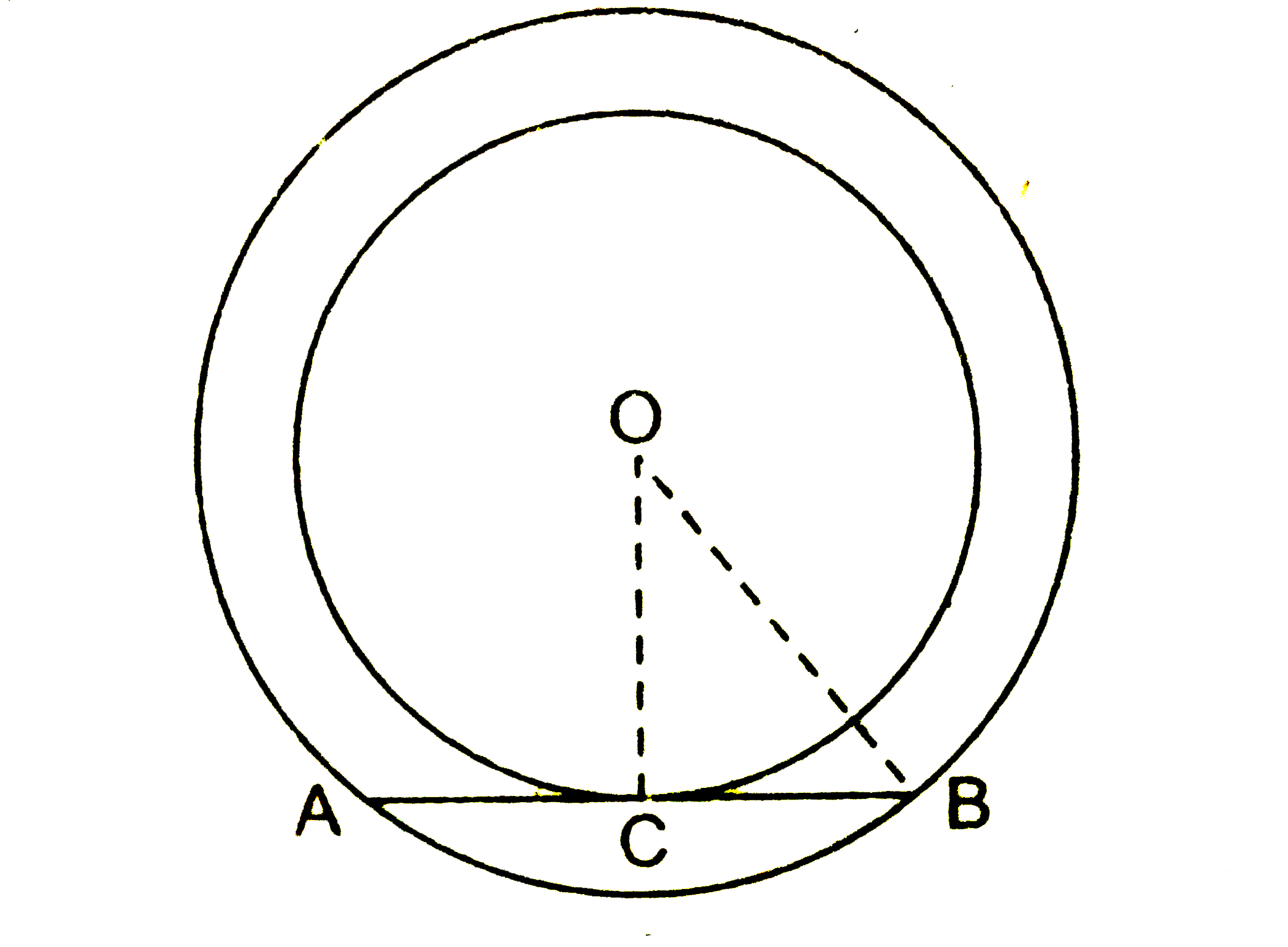
Two circles joinedat 'C'. Chord AB of the large circle touches the small circle at
M. Radius of the small circle is,r and of the large circle is 'R'. If 'M A=M B=a', prove that 'a^2=4 r(R-r)'.
'(##VPU_TTT_MAT_X_P02_C07_E10_007_Q01##)'Solution in Malayalam
Step by step video solution for Two circles joinedat 'C'. Chord AB of the large circle touches the small circle at M. Radius of the small circle is,r and of the large circle is 'R'. If 'M A=M B=a', prove that 'a^2=4 r(R-r)'. '(##VPU_TTT_MAT_X_P02_C07_E10_007_Q01##)' by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The distance covered by an athlete in lóng jump-practice are
'6.10,6.20,6.18,6.20,6.25,6.21,6.15,6.10'
in metres. Find the mean and median. Why is it that there is not much differerice between these?
View SolutionIn the triangle shown, what is the perpendicular distance from the top vertex to the bottom side? What is the area of the triangle?
'(##VPU_TTT_MAT_X_P01_C05_E01_001_Q01##)'
View SolutionA circle of radius R touches externally a set of 12 circles each of radius r surrounding it.Each one of the smaller circles touches two circles of the set,then ((R)/(r))=sqrt(m)+sqrt(n)-1 where m,n in N and m+n is
View SolutionA circle of radius R touches externally a set of 12 circles each of radus r surronding it. Each one of the smaller circles touches two circles of the set.Then (R)/(r)=sqrt(m)+sqrt(n)-1 where m,n in N and m+n is
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance (r)/(2) from O, then /_BAO=
View SolutionIf inside a big circle exactly n(n≤3) small circles, each of radius r, can be drawn in such a way that each small circle touches the big circle and also touches both its adjacent small circles, then the radius of big circle is r(1+cosecπn) (b) (1+tanπncosππ) r[1+cosec2πn] (d) r[s∈π2n+cos(2π)n]2sinπn
View SolutionIn Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
View SolutionA circle of radius R touches externally a set of 12 circles each of radius r surrounding it.Each one of the smaller circles touches two circles of the set.Then (R)/(r)=sqrt(m)+sqrt(n)-1, where m,n in N and m+n is
View Solution) and In this figure two bigger circles C(0,r) and C(O',r') touch each other.On third circle C(0,r) are touching the two bigger circles as well as the common tangent.Then prove
View SolutionCircles of radii 2,2,1 touch each other externally.If a circle of radius r touches all the three circles externally,then r is
View Solution15 सेमी और 17 सेमी त्रिज्या के दो समकेन्द्रीय वृत्त हैं। यदि बड़े वृत की जीवा AB अन्दर वाले वृत्त हैं। यदि बड़े वृत्त की जीवा AB अन्दर वाले वृत्त को बिन्दु C पर स्पर्श करती हैं, तो जीवा AB की माप ज्ञात कीजिए।
View SolutionFind the rate of change of the area of a circle with respect to its radius r when(a) r=3cm (b) r=4cm
View SolutionIf inside a big circle exactly n(n≤3) small circles, each of radius r, can be drawn in such a way that each small circle touches the big circle and also touches both its adjacent small circles, then the radius of big circle is r(1+cosecπn) (b) (1+tanπncosππ) r[1+cosec2πn] (d) r[s∈π2n+cos(2π)n]2sinπn
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionThe radius R Find the point of the center of a circle, if this circle, R The outer circle touches the second circle of radius.
View SolutionIn the figure, O is the centre of both the circles. AB and AC touch the small circle at P and Q.A,B and C are points on the large circle.
Prove that Ab=AC.
 .
.
View Solution
