In the figure, AC is a tangent to the circle with centre O . More over, 'B C' is the perpendicular from 'C' to OA. If the radius of the circle be 'r', prove that 'OA xx OB=r^2'.
'(##VPU_TTT_MAT_X_P02_C07_E15_001_Q01##)'Solution in Malayalam
Step by step video & image solution for In the figure, AC is a tangent to the circle with centre O . More over, 'B C' is the perpendicular from 'C' to OA. If the radius of the circle be 'r', prove that 'OA xx OB=r^2'.'(##VPU_TTT_MAT_X_P02_C07_E15_001_Q01##)' by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The distance covered by an athlete in lóng jump-practice are
'6.10,6.20,6.18,6.20,6.25,6.21,6.15,6.10'
in metres. Find the mean and median. Why is it that there is not much differerice between these?
View SolutionIn the triangle shown, what is the perpendicular distance from the top vertex to the bottom side? What is the area of the triangle?
'(##VPU_TTT_MAT_X_P01_C05_E01_001_Q01##)'
View SolutionIn Figure, OA and OB ar respectively perpendiculars to chords CD and EF of a circle whose centre is O. If OA=OB , prove that CE=DF.

View SolutionConsider the circle: x^2+y^2=r^2 with centre O. A and B are collinear with O such that OA. OB=r^2. The number of circles passing through A and B, which are orthogonal to the circle C is
View SolutionTangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
View SolutionIf OA and OB are the tangents from the origin to the circle x^(2)+y^(2)+2gx+2fy+c=0 and C is the centre of the circle,the area of the quadrilateral OACB is
View SolutionFind the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

View SolutionIn the figure below, CD is a chord of the semi circle with centre O.
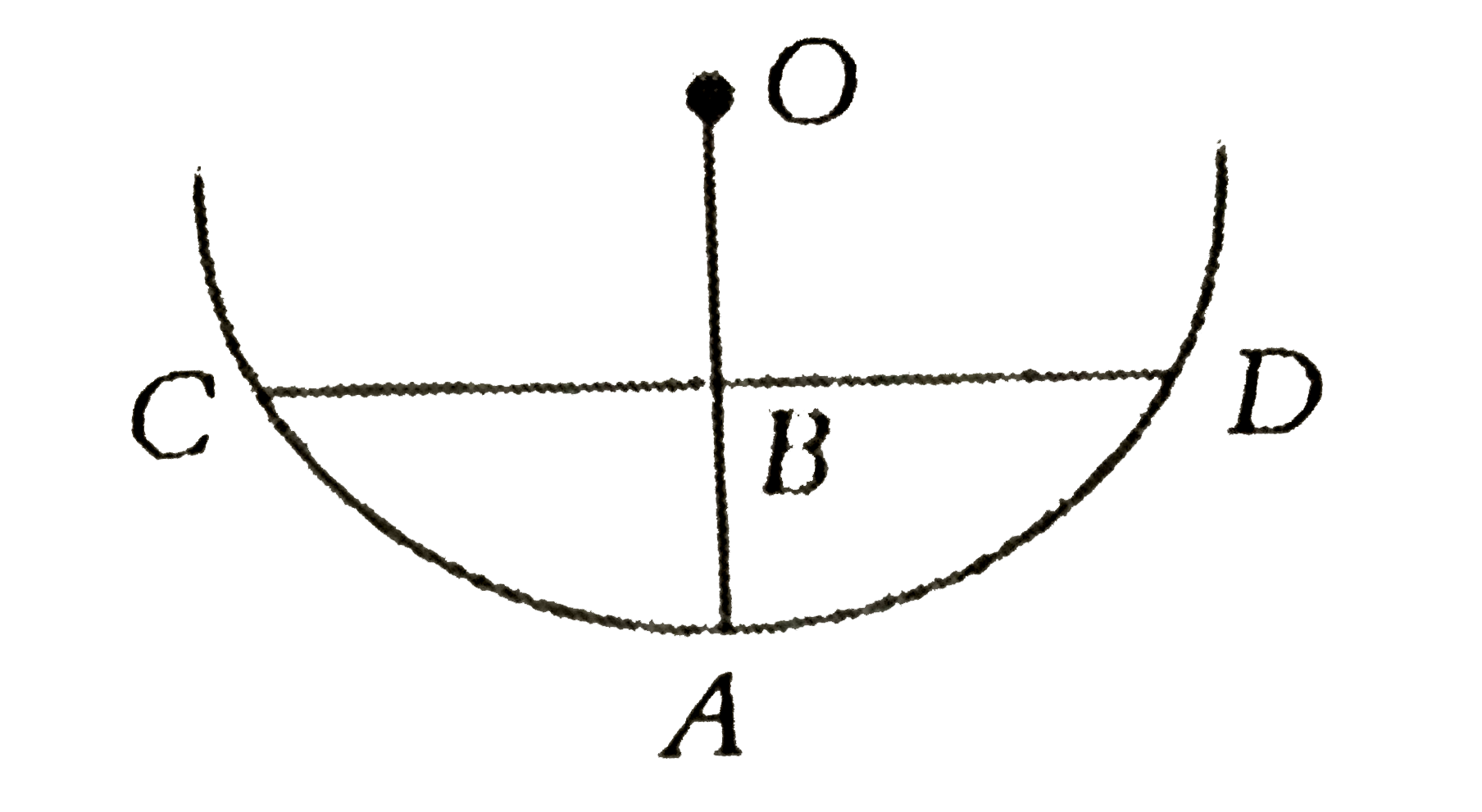 OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
OA is the radius of the circle. If CD=10 cm, AB=2 cm and ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯CD the length of OB is _____________
View SolutionIf OA and OB are the tangent from the origin to the circle x2+y2+2gx+2fy+c=0andC is the centre of the circle then the area of the quadrilateral OCAB is
View SolutionOA and OB are tangents drawn from the origin O to the circle x2+y2+2gx+2fy+c=0 where c > 0, C being the centre of the circle. Then ar (quad. OACB) is:
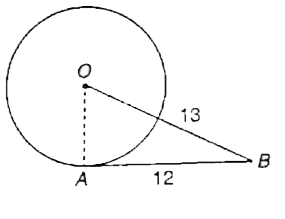
View SolutionIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
View Solutionवक्तव्य । चित्रानुसार सदिशों OA, OB एवं OC का परिणामी R(1+√2)है। R वृत्त की त्रिज्या है।
वक्तव्य || OA+OC,OB के अनुदिश है तथा (OA+OC)+OB,OB के अनुदिश है।

View SolutionIf OA and OB circle x^(2) + y^(2) - 2x + 4y = 0 Is the equation of OA and OB, where O is the pivot.
View SolutionA,B are conjugate points w.r.t circle having centre O radius r then OA2+OB2−2r2=AB2
View SolutionIf polars of A,B w.r.t to the circle having centre O and radius r intersect at P then OA2−OB2=AP2−BP2
View SolutionA and B are two points on the hyperbola O is the centre. If OA is perpendicular to OB then 1(OA)2+1(OB)2 is equal to
View Solution
