Two persons A and B wear glasses of optical powers (in air) P1=+2D and P2=+1D respectively. The glasses have refractive index 1.5. Now they jump into a swimming pool and look at each other. B appears to be present at distance 2m (f rom A) to A. A appears to be present at distance 1m (from B) to B. The refractive index of water in the swimming pool, in the form X10 and find X.
To solve the problem, we need to find the refractive index of water in the swimming pool, given the optical powers of glasses worn by two persons A and B, and the distances at which they appear to each other when submerged in water.
1. Identify the Given Data:
- Optical power of A, P1=+2D
- Optical power of B, P2=+1D
- Refractive index of the glasses, nglass=1.5
- Distance B appears to A, dAB=2m=200cm
- Distance A appears to B, dBA=1m=100cm
2. Calculate the Focal Lengths of the Glasses:
- The focal length f is related to optical power P by the formula:
f=1P
- For A:
f1=1P1=12m=50cm
- For B:
f2=1P2=11m=100cm
3. Set Up the Lens Maker's Formula:
- The lens maker's formula in air is:
1f=(nglass−1)(1R1−1R2)
- For A in air:
1f1=(1.5−1)(1R1−1R2)⟹150=12(1R1−1R2)
- For B in air:
1f2=(1.5−1)(1R1−1R2)⟹1100=12(1R1−1R2)
4. Calculate the Focal Lengths in Water:
- When they jump into the water, the effective focal lengths change. The new formula becomes:
1f′=(nglass−nwater)(1R1−1R2)
- Let nwater be the refractive index of water. We can express it as:
1f′1=(1.5−nwater)(1R1−1R2)
- Similarly for B:
1f′2=(1.5−nwater)(1R1−1R2)
5. Use the Image Formation Formula:
- For A:
1v−1u=1f′1
Where v=−200cm (image distance) and u=−x (object distance).
- For B:
1v−1u=1f′2
Where v=−100cm and u=−x.
6. Set Up the Equations:
- From A:
1−200−1−x=1f′1
- From B:
1−100−1−x=1f′2
7. Solve the System of Equations:
- Equate the two expressions for 1f′ derived from A and B.
- Substitute the values of f′1 and f′2 in terms of nwater.
8. Find the Value of nwater:
- After solving the equations, you will find:
nwater=65
9. Express in the Required Form:
- The refractive index of water can be expressed as:
nwater=X10⟹X=12
Final Answer:
Thus, the value of X is 12.
- Optical power of A, P1=+2D
- Optical power of B, P2=+1D
- Refractive index of the glasses, nglass=1.5
- Distance B appears to A, dAB=2m=200cm
- Distance A appears to B, dBA=1m=100cm
- The focal length f is related to optical power P by the formula:
f=1P
- For A:
f1=1P1=12m=50cm
- For B:
f2=1P2=11m=100cm
- The lens maker's formula in air is:
1f=(nglass−1)(1R1−1R2)
- For A in air:
1f1=(1.5−1)(1R1−1R2)⟹150=12(1R1−1R2)
- For B in air:
1f2=(1.5−1)(1R1−1R2)⟹1100=12(1R1−1R2)
- When they jump into the water, the effective focal lengths change. The new formula becomes:
1f′=(nglass−nwater)(1R1−1R2)
- Let nwater be the refractive index of water. We can express it as:
1f′1=(1.5−nwater)(1R1−1R2)
- Similarly for B:
1f′2=(1.5−nwater)(1R1−1R2)
- For A:
1v−1u=1f′1
Where v=−200cm (image distance) and u=−x (object distance).
- For B:
1v−1u=1f′2
Where v=−100cm and u=−x.
- From A:
1−200−1−x=1f′1
- From B:
1−100−1−x=1f′2
- Equate the two expressions for 1f′ derived from A and B.
- Substitute the values of f′1 and f′2 in terms of nwater.
- After solving the equations, you will find:
nwater=65
- The refractive index of water can be expressed as:
nwater=X10⟹X=12
Thus, the value of X is 12.
Topper's Solved these Questions
Similar Questions
The refractive index of glass is 1.5. The speed of light in glass is
View SolutionThe refractive index of glass is 1.5. Find the speed of light in glass.
View SolutionA mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View SolutionRefractive index of glass with respect to water is (9/8).
Refractive index of glass with respect to air is (3/2). find the refractive index of water with respect to air .View SolutionA person wears glases of power -2.5 D. The defect of the eye and far point of the person without glasses are respectively
View SolutionThe least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
View SolutionThe least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
View SolutionAn equiconvex lens is made from glass of refractive index 1.5. If the radius of each surface is changed from 5cm to 6cm, then the power
View SolutionThe refractive index of glass with respect to air is 1.5. What is the value of the refractive index of air with respect to glass?
View SolutionRefractive index of the glass slab is 1.5. There is a point object O inside the slab as shown. To eyeE1 object appears at a distance of 6cm (From the top surface) and to eye E2 it appears at a distance of 8cm (from the bottom surface). Find thickness of the glass slab.
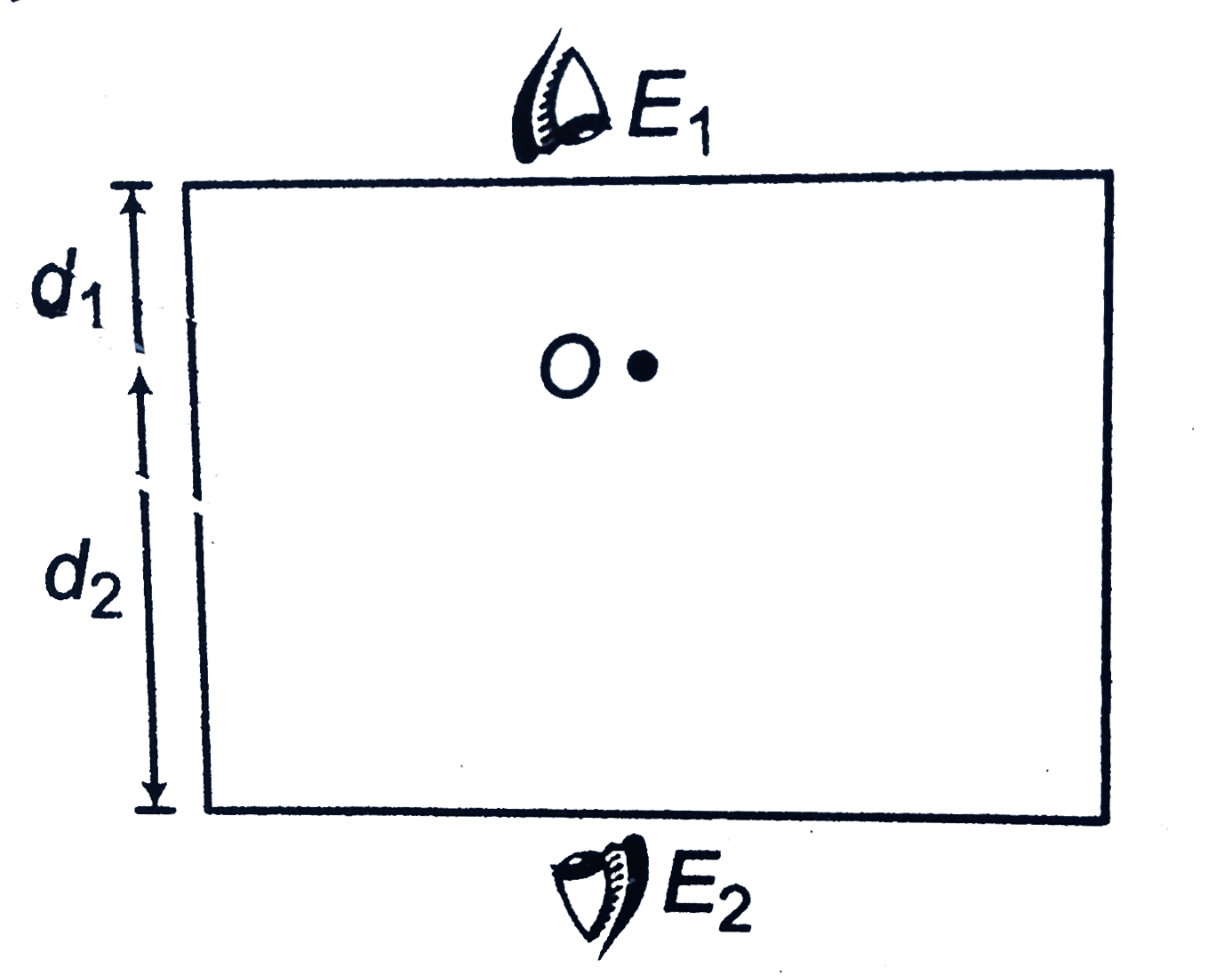 View Solution
View Solution

