A charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. The potential energy of the system in first situation where the charge is divided into three equals parts is
14πεoq2r
136πεoq2r
112√3πεoq2r
112πεoq2r
To solve the problem, we need to calculate the potential energy of a system where a charge Q is divided into three equal parts and placed symmetrically on a circle of radius r.
1. Divide the Charge:
The total charge Q is divided into three equal parts:
q1=q2=q3=Q3
2. Position of Charges:
The charges are placed symmetrically on the circle, forming the vertices of an equilateral triangle. The distance from the center of the circle to each vertex (where the charges are placed) is the radius r.
3. Calculate the Side Length:
The side length A of the equilateral triangle formed by the charges can be related to the radius r using the formula:
A=√3r
4. Potential Energy Between Each Pair:
The potential energy U between two point charges q1 and q2 separated by a distance r is given by:
U=kq1q2d
where k is Coulomb's constant (k=14πϵ0) and d is the distance between the charges.
5. Calculate Potential Energy for Each Pair:
For our system, we have three pairs of charges:
- Pair 1: (q1,q2)
- Pair 2: (q2,q3)
- Pair 3: (q1,q3)
The potential energy for each pair is:
U12=U23=U31=k(Q3)(Q3)A=kQ2/9A
6. Total Potential Energy:
Since there are three pairs, the total potential energy Utotal is:
Utotal=3⋅U12=3⋅kQ2/9A=kQ23A
7. Substituting the Value of A:
Now substitute A=√3r:
Utotal=kQ23√3r
8. Substituting the Value of k:
Finally, substituting k=14πϵ0:
Utotal=Q24πϵ0⋅13√3r=Q212√3πϵ0r
Final Answer:
The potential energy of the system when the charge Q is divided into three equal parts and placed symmetrically on a circle of radius r is:
Utotal=Q212√3πϵ0r
The total charge Q is divided into three equal parts:
q1=q2=q3=Q3
The charges are placed symmetrically on the circle, forming the vertices of an equilateral triangle. The distance from the center of the circle to each vertex (where the charges are placed) is the radius r.
The side length A of the equilateral triangle formed by the charges can be related to the radius r using the formula:
A=√3r
The potential energy U between two point charges q1 and q2 separated by a distance r is given by:
U=kq1q2d
where k is Coulomb's constant (k=14πϵ0) and d is the distance between the charges.
For our system, we have three pairs of charges:
- Pair 1: (q1,q2)
- Pair 2: (q2,q3)
- Pair 3: (q1,q3)
U12=U23=U31=k(Q3)(Q3)A=kQ2/9A
Since there are three pairs, the total potential energy Utotal is:
Utotal=3⋅U12=3⋅kQ2/9A=kQ23A
Now substitute A=√3r:
Utotal=kQ23√3r
Finally, substituting k=14πϵ0:
Utotal=Q24πϵ0⋅13√3r=Q212√3πϵ0r
The potential energy of the system when the charge Q is divided into three equal parts and placed symmetrically on a circle of radius r is:
Utotal=Q212√3πϵ0r
Topper's Solved these Questions
Similar Questions
A charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. The ratio of electric potentials at the centre in the two situations isView SolutionA charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. If a charge (part charge) is removed from one location in both the situations, the ratio of magnitudes of the electric field intensities at the centre isView SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionThree dipoles each of dipole moment of magnitude p are placed tangentially on a circle of radius R in its plae positioned at equal angle from each other as shown in the figure. Then the magnitude of electric field intensity at the centre of the circle will be :
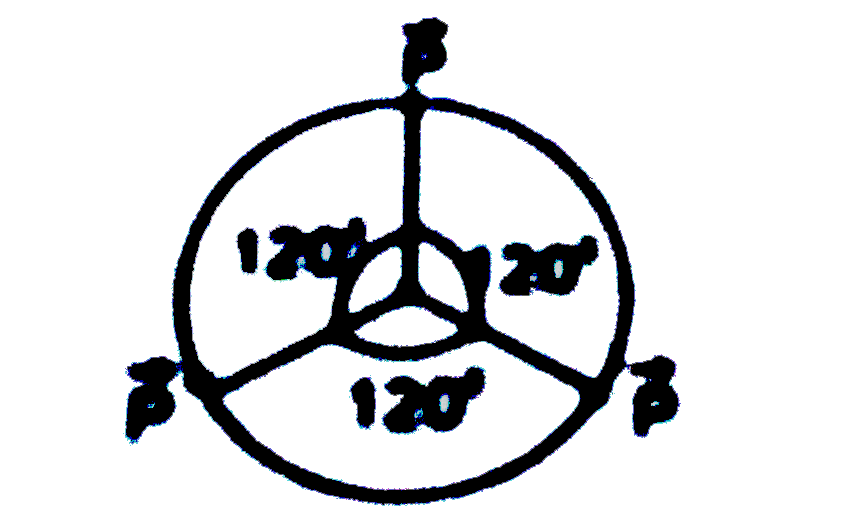 View Solution
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionEight equal point charges are placed at corners of a cube side length a. The potential and electric field magnitude at the centre of cube will be
View SolutionA conducting shell of radius R carries charge–Q. A point charge +Q is placed at the centre of shell. The electric field E varies with distance r (from the centre of the shell) as :
View SolutionTwo equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.
 View Solution
View Solution

