Column I lists the field in a region and Column II lists the path of a charge q and mass m on which the particle can move Match the proper entries from column-2 to column -1 using the codes given below the columns, [Consider all fields to be uniform]
ColumnI ColumnII(P)Only electric field →E is present(1)The particle can move on a straigth line(Q)Only magnrtic field →B is present(2)The particle can move on a circle(R)Only gravitional field →g is present(3)The particle can move on parabolic path(S)Both electric field →E and magnetic field(4)The particle can remain in rest
(P)(Q)(R)(S)4312
(P)(Q)(R)(S)3142
(P)(Q)(R)(S)3214
(P)(Q)(R)(S)1231
To solve the problem, we need to match the fields in Column I with the corresponding paths of a charge q and mass m in Column II. Let's analyze each entry in Column I step by step.
Step 1: Analyze the Electric Field (Column I: P)
- Field: Only electric field →E is present.
- Force on the charge: The force acting on the charge q due to the electric field is given by →F=q→E.
- Motion: Since the force is constant (uniform electric field), the charge will accelerate in the direction of the electric field. Thus, the charge will move in a straight line.
Match: P → 1 (The particle can move on a straight line).
Step 2: Analyze the Magnetic Field (Column I: Q)
- Field: Only magnetic field →B is present.
- Force on the charge: The magnetic force acting on the charge moving with velocity →v in a magnetic field is given by →F=q(→v×→B).
- Motion: The magnetic force is always perpendicular to the velocity of the charge, causing it to move in a circular path.
Match: Q → 2 (The particle can move on a circle).
Step 3: Analyze the Gravitational Field (Column I: R)
- Field: Only gravitational field →g is present.
- Motion: When a charge is projected in a gravitational field, it follows a parabolic trajectory due to the influence of gravity acting downwards while it has an initial horizontal velocity.
Match: R → 3 (The particle can move on a parabolic path).
Step 4: Analyze Both Electric and Magnetic Fields (Column I: S)
- Field: Both electric field →E and magnetic field →B are present.
- Motion: When both fields are acting on the charge, the net force can result in a straight-line motion if the electric and magnetic forces balance each other out in such a way that the charge moves in a straight line.
Match: S → 4 (The particle can remain in rest).
Final Matches
- P → 1
- Q → 2
- R → 3
- S → 4
Summary of Matches
- P: Only electric field →E is present → 1: The particle can move on a straight line.
- Q: Only magnetic field →B is present → 2: The particle can move on a circle.
- R: Only gravitational field →g is present → 3: The particle can move on a parabolic path.
- S: Both electric field →E and magnetic field →B are present → 4: The particle can remain in rest.
- Field: Only electric field →E is present.
- Force on the charge: The force acting on the charge q due to the electric field is given by →F=q→E.
- Motion: Since the force is constant (uniform electric field), the charge will accelerate in the direction of the electric field. Thus, the charge will move in a straight line.
- Field: Only magnetic field →B is present.
- Force on the charge: The magnetic force acting on the charge moving with velocity →v in a magnetic field is given by →F=q(→v×→B).
- Motion: The magnetic force is always perpendicular to the velocity of the charge, causing it to move in a circular path.
- Field: Only gravitational field →g is present.
- Motion: When a charge is projected in a gravitational field, it follows a parabolic trajectory due to the influence of gravity acting downwards while it has an initial horizontal velocity.
- Field: Both electric field →E and magnetic field →B are present.
- Motion: When both fields are acting on the charge, the net force can result in a straight-line motion if the electric and magnetic forces balance each other out in such a way that the charge moves in a straight line.
- P → 1
- Q → 2
- R → 3
- S → 4
- P: Only electric field →E is present → 1: The particle can move on a straight line.
- Q: Only magnetic field →B is present → 2: The particle can move on a circle.
- R: Only gravitational field →g is present → 3: The particle can move on a parabolic path.
- S: Both electric field →E and magnetic field →B are present → 4: The particle can remain in rest.
Topper's Solved these Questions
Similar Questions
In column-II, some situations are given, and in column-I, their results are given. Mathc the proper entries from column-2 to column-1 using the codes iven below the columns

View SolutionIn each situation of column-I,a process A→B→C is given for an ideal gas. Match the proper entries from column-2 to column-1 using the codes given below the columns
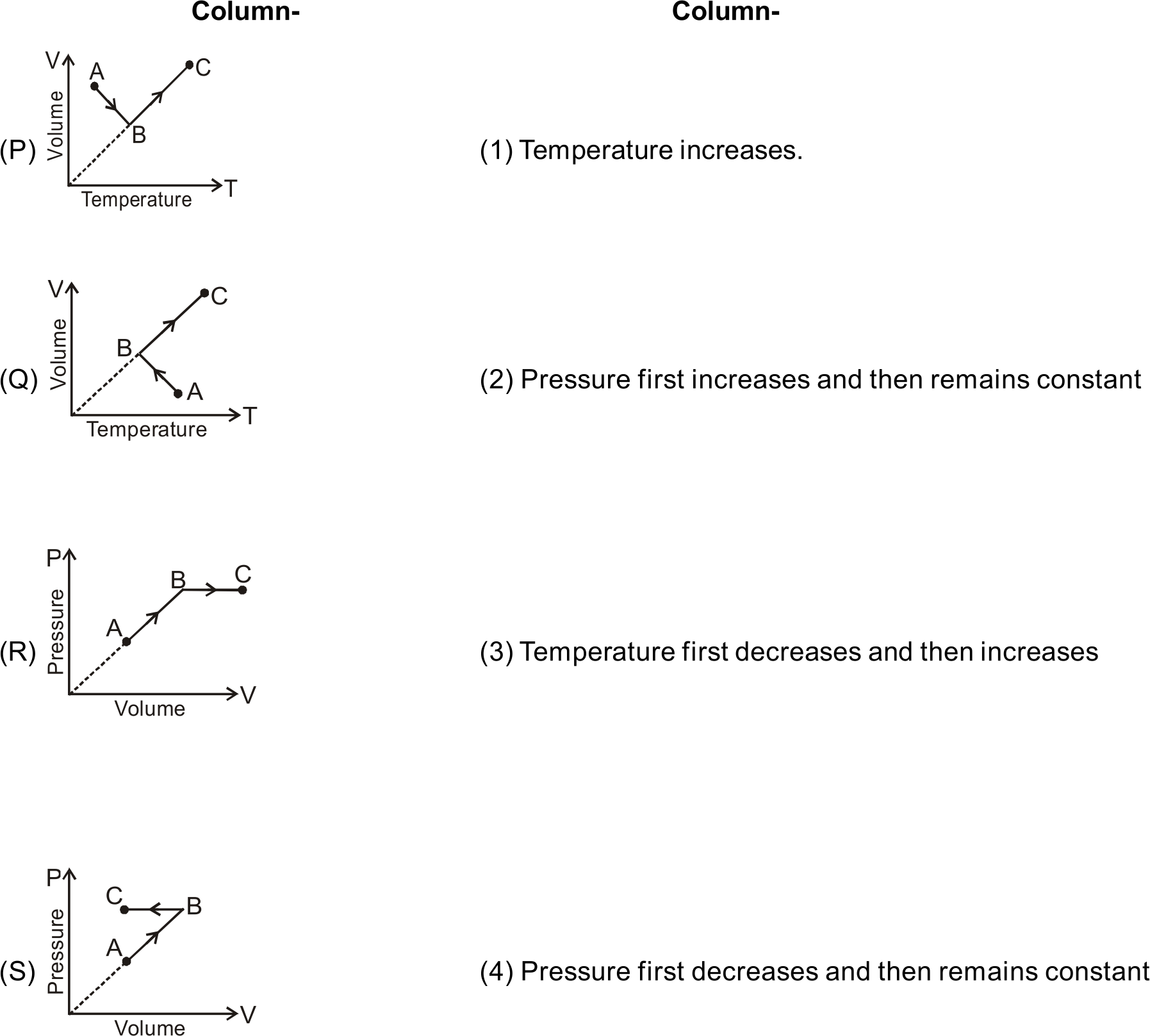
View SolutionMatch the entries of Column I with those of Column-II

View SolutionMatch the entries of Column I with those of Column-II

View SolutionColumn I lists some properties of waves and Column II lists the factors on which they depend . Match the entries in Column I with those in Column II.

View SolutionMatch Column-I with Column-II and select the correct answer using the code given below the Columns

View SolutionColumn I lists the endocrine structure and Column II lists corresponding hormones. Match the two columns and identify the correct option from those given
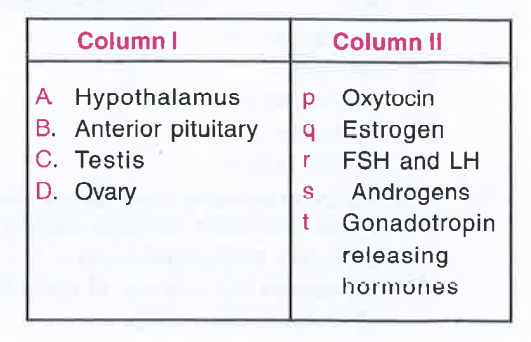
View SolutionColumn II lists some expression of force and potential energy. Match the entries in column I with the expression in column II.

View SolutionMatch all the entries in column-I to all the entries in column-II

View SolutionColumn I list the parts of the human brain and column II lists the functions. Match the two columns and identify the correct choice from those given
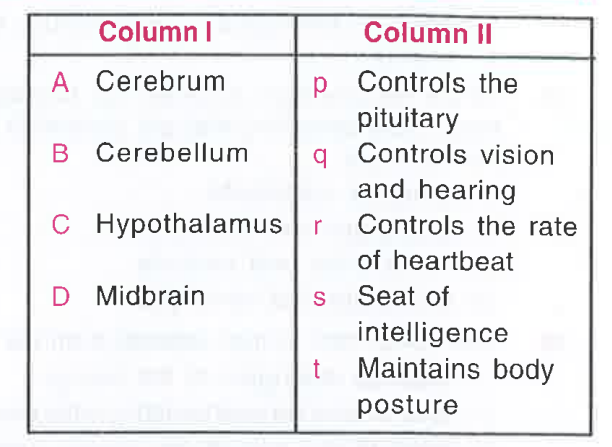
View Solution
