Time varying magnetic filed is present in a circular region of radius R. Match the proper entries from column-2 to column-1 using the codes given below the columns,
Column IColumn II(P) An unsteady magnetic field(1) Electric field is perpendicular to the length of rod (Q)Induced electric field at a point within magnetic field (r gtR)(2)r2dBdt(R)Induced electric field at a point out side the magnetic field (r lt R)(3)R22rdBdt(S)If a rod is placed along the diameter of the magnetic field(4) induced electric field
PQRS(A)3214
PQRS(B)2134
PQRS(C)4213
PQRS(D)4231
To solve the problem, we need to match the entries from Column I with the correct entries from Column II based on the principles of electromagnetism, particularly the behavior of electric fields in the presence of a time-varying magnetic field.
1. Identify the entries in Column I and Column II:
- Column I:
- (P) An unsteady magnetic field
- (Q) Induced electric field at a point within magnetic field (r > R)
- (R) Induced electric field at a point outside the magnetic field (r < R)
- (S) If a rod is placed along the diameter of the magnetic field
- Column II:
- (1) Electric field is perpendicular to the length of the rod
- (2) r2dBdt
- (3) R22rdBdt
- (4) Induced electric field
2. Match (P) An unsteady magnetic field:
- An unsteady (time-varying) magnetic field induces an electric field. Therefore, we match (P) with (4) "Induced electric field."
- Match: (P) → (4)
3. Match (Q) Induced electric field at a point within magnetic field (r > R):
- For points within the magnetic field (where r > R), the induced electric field can be calculated using the formula:
E=r2dBdt
- Match: (Q) → (2)
4. Match (R) Induced electric field at a point outside the magnetic field (r < R):
- For points outside the magnetic field (where r < R), the induced electric field can be calculated using:
E=R22rdBdt
- Match: (R) → (3)
5. Match (S) If a rod is placed along the diameter of the magnetic field:
- If a rod is placed along the diameter of the magnetic field, the induced electric field will be perpendicular to the length of the rod.
- Match: (S) → (1)
Final Matches:
- (P) → (4)
- (Q) → (2)
- (R) → (3)
- (S) → (1)
- Column I:
- (P) An unsteady magnetic field
- (Q) Induced electric field at a point within magnetic field (r > R)
- (R) Induced electric field at a point outside the magnetic field (r < R)
- (S) If a rod is placed along the diameter of the magnetic field
- (1) Electric field is perpendicular to the length of the rod
- (2) r2dBdt
- (3) R22rdBdt
- (4) Induced electric field
- An unsteady (time-varying) magnetic field induces an electric field. Therefore, we match (P) with (4) "Induced electric field."
- Match: (P) → (4)
- For points within the magnetic field (where r > R), the induced electric field can be calculated using the formula:
E=r2dBdt
- Match: (Q) → (2)
- For points outside the magnetic field (where r < R), the induced electric field can be calculated using:
E=R22rdBdt
- Match: (R) → (3)
- If a rod is placed along the diameter of the magnetic field, the induced electric field will be perpendicular to the length of the rod.
- Match: (S) → (1)
- (P) → (4)
- (Q) → (2)
- (R) → (3)
- (S) → (1)
Topper's Solved these Questions
Similar Questions
In column-II, some situations are given, and in column-I, their results are given. Mathc the proper entries from column-2 to column-1 using the codes iven below the columns
 View Solution
View SolutionElectric field induced by changing magnetic fields are
View Solution
The electric field at r= R isView SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png) View Solution
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionFigure shows a circular region of radius R in which uniform magnetic field B exists. The magnetic field is increasing at a rate dBdt. The induced electric field at a distance r from the centre for r<R is
 View Solution
View SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
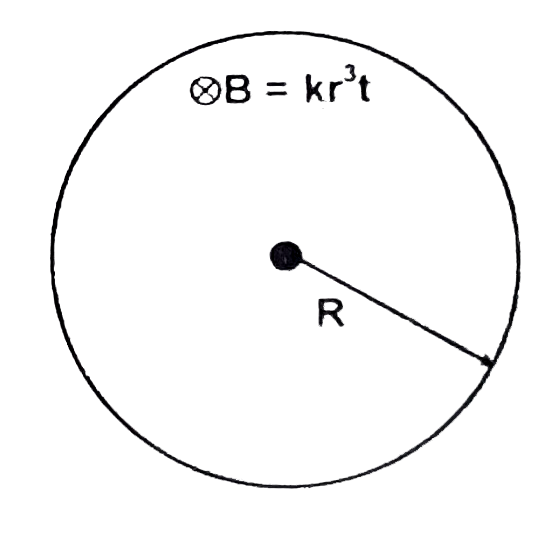 View Solution
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
 View Solution
View SolutionCan a photon be deflected by an electric field ? By a magnetic field ?
View SolutionIf a chraged particle at rest experiences no electromagnetic force,
(i) the electric field must be zero
(ii) the magnetic field must be zero
(iii) the electric field may or may not be zero
(iv) the magnetic field may or may not be zeroView Solution

