Show that Reynold's number R=ρv0dη is dimensionless. (ρ is density of the fluid, v0 is the critical velocity, d is diameter through which the fluid is flowing and η is the coefficient of viscosity of the fluid).
R=[ML−3][LT−1][L][ML−1T−1]=[ML−1T−1ML−1T−1]=[M0L0T0]
∴R is dimensionless.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IA
175 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IB (ASSERTION & REASON)
46 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
108 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
Similar Questions
When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
A. 1.3m/s
B. 3.4m/s
C. 5.2m/s
D. 6.5m/s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−3m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?
View Solution
Knowledge Check
When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−2m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?A2×10−3Pa−sB1×10−3Pa−sC4×10−3Pa−sD5×10−4Pa−sWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−sA0.5m/sB1.0m/sC1.5m/sD2.0m/sIf V1 and V2D be the volumes of the liquids flowing out of the same tube in the same interval of time and η1 and η2 their coefficients of viscosity respectively then
Aη1η2=V2V1Bη1η2=V1V2Cη1η2=V21V22Dη1η2=V22V21
Check the correctness of the equation v=Kηrρ using dimensional analysis, where v is the critical velocity η is the coefficient of viscosity, r is the radius and ρ is the density?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−s
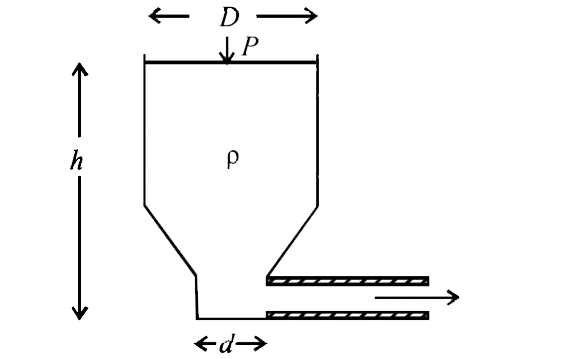
View SolutionShown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η.
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View Solution
