Find the Q-value and the kinetic energy of the emitted α particle in the α-decay of (a) 22688 Ra and (b)22086 Rn
Given m (22688Ra ) = 226.02540 u, m (22286 Rn ) = 222.01750 u,
m ( 22286 Rn ) = 220.01137 u, m (22684 Po) = 216.00189 u.
Q=[M(Ra226−M(Rn222)−M(He4)]×931
=(226.025406−222.017574−4.002603)u×931
=0.005229u×931Mevu
Q=4.87 MeV
Topper's Solved these Questions
Similar Questions
The kinetic energy of α-particle emitted in the α-decay of 88Ra266 is [given, mass number of Ra = 222 u]
View SolutionIdentify whether the given transformation is an alpha decay or beta decay (226)Ra to (222)Rn,,,
View SolutionThe .22688Ra nucleus undergoes α-decay to .22286Rn. Calculate the amount of energy liberated in this decay. Take the mass of .22688Ra to be 226.025402u, that of .22688Rn to be 222.017571u, and that of .42He to be 4.002602u.
View SolutionThe kinetic energy of α- particles emiited in the decay of .88Ra226 into .86Rn222 is measured to be 4.78MeV. What is the total disintegration energy or the 'Q'-value of this process ?
View SolutionThe number of α particles emitted per second by 1g of 88226 Ra is 3.7×1010. The decay constant is :
View SolutionConsider the following nuclear fission reaction
.88Ra226→.86Rn222+.2He4+Q
In the fission reaction. Kinetic energy of α-particle is 4.44 MeV. Find the energy emitted as γ-radiation in keV in this reaction.
m(.88Ra226)=226.005 amu
m(.86Rn222)=222.000 amuView SolutionUranium ores contain one radium −226atom for every 2.8×106 uranium −238 atoms. Calculate the half-life of .88Ra226 is 1600 years (.88Ra226 is a decay product of .92U238).
View SolutionThe nucleus of .23090Th is unstable against α-decay with a half-life of 7.6×103years. Write down the equation of the decay and estimate the kinetic energy of the emitted α-particle from the following data: m(.23090Th)=230.0381amu,m(.22668Ra)=226.0254amum(.42He)=4.0026amu.
View SolutionObtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
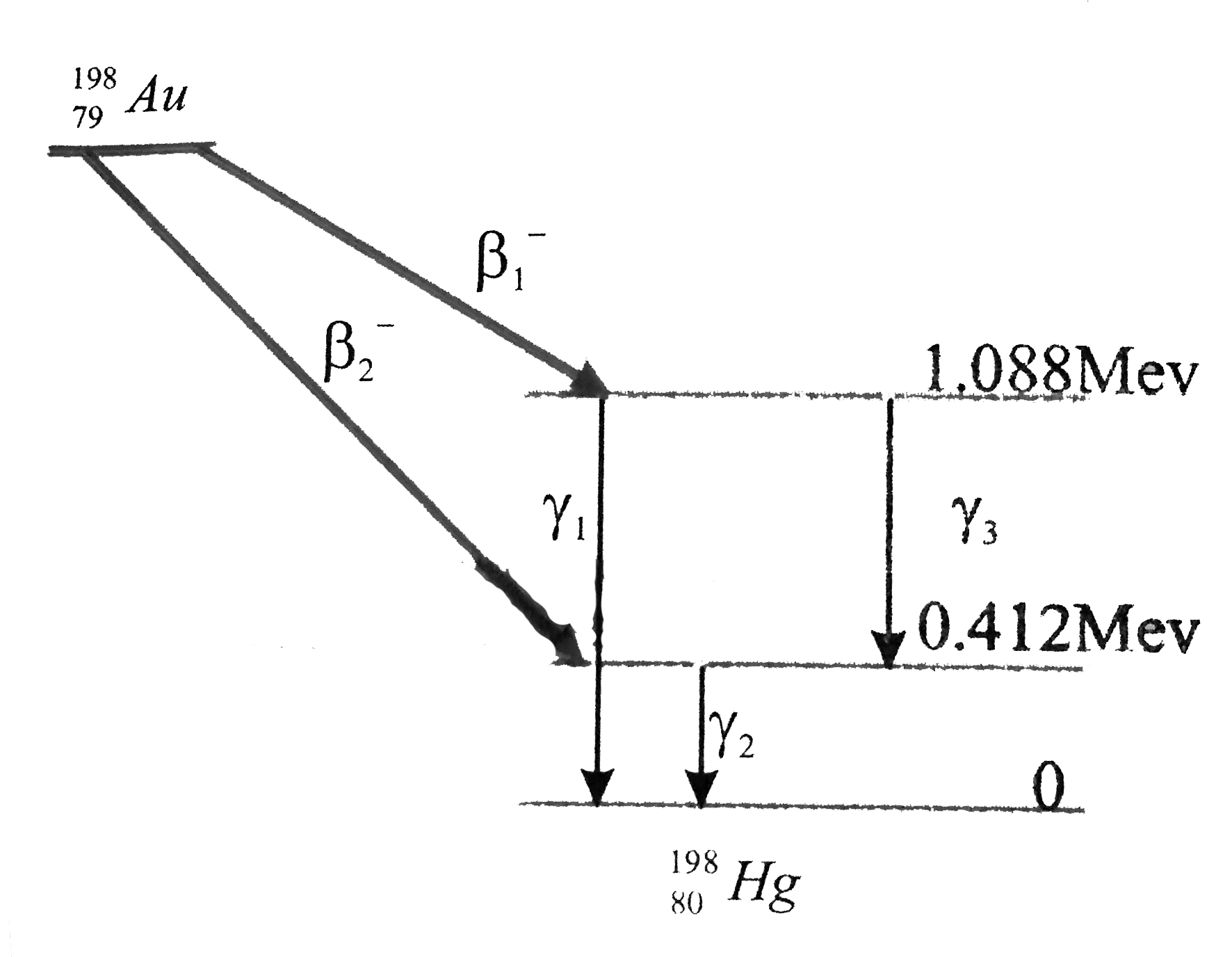View SolutionWhat is the significance of binding energy per nucleon of a nucleus ?
(ii) in a certain star, three alpha particles undergo fusion in a single reaction to form 126C nucleus. Calculate the energy released in this reaction in MeV.
Given : m(42He)=4.002604u and m(126C)=12.000000uView Solution