A straight line source of sound of length , emits a pulse of sound energy (in mW) is intercepted by an acoustic cylindrical detector of surface area . Located at a perpendicular distance 7 m from the source ? The waves reach perpenduculary at the surface of the detector. The total emiited by the source in the form of sound is . (use )
To solve the problem, we need to calculate the power received by the acoustic cylindrical detector from the straight line source of sound. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the parameters given
- Length of the sound source, L=10m
- Distance from the source to the detector, r=7m
- Surface area of the detector, A=2.4cm2=2.4×10−4m2
- Total power emitted by the source, P=2.2×104W
Step 2: Calculate the intensity of the sound at the distance r
The intensity I at a distance r from a line source can be calculated using the formula:
I=P2πrL
Substituting the values:
I=2.2×1042π(7)(10)
Using π≈227:
I=2.2×1042×227×7×10
I=2.2×1042×22×10
I=2.2×104440
I=50W/m2
Step 3: Calculate the power received by the detector
The power Pd received by the detector can be calculated using the formula:
Pd=I×A
Substituting the values:
Pd=50×2.4×10−4
Pd=12×10−4W
Pd=1.2×10−3W=1.2mW
Final Answer
The power received by the acoustic cylindrical detector is 1.2mW.
---
- Length of the sound source, L=10m
- Distance from the source to the detector, r=7m
- Surface area of the detector, A=2.4cm2=2.4×10−4m2
- Total power emitted by the source, P=2.2×104W
The intensity I at a distance r from a line source can be calculated using the formula:
I=P2πrL
Substituting the values:
I=2.2×1042π(7)(10)
Using π≈227:
I=2.2×1042×227×7×10
I=2.2×1042×22×10
I=2.2×104440
I=50W/m2
The power Pd received by the detector can be calculated using the formula:
Pd=I×A
Substituting the values:
Pd=50×2.4×10−4
Pd=12×10−4W
Pd=1.2×10−3W=1.2mW
The power received by the acoustic cylindrical detector is 1.2mW.
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA source emitting sound of frequency 180 Hz is alced in front of a wall at a distance of 2 m from it. A detector is also placed in front of the weal at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360ms−1.

View SolutionA source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170ms−1. A detector is placed at a distance of 200 m from the line of motion of the source. (a) Find the frequency of sound received by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant it detects the frequency 1200 Hz. Velocity of sound in air=340ms−1.
View SolutionA source emitting sound of frequency 180Hz is placed in front of a wall at distance of 2m from it . A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360m/s.
View SolutionA straight line source of sound of length L=10m, emits a pulse of sound energy (in mW) is intercepted by an acoustic cylindrical detector of surface area 2.4cm2. Located at a perpendicular distance 7 m from the source ? The waves reach perpenduculary at the surface of the detector. The total emiited by the source in the form of sound is 2.2×104W. (use π=22/7)
View SolutionStatement-1: The change in pitch of sound depends on speed of source and detector relative to each other and not on the distance between them. Statement-2: The pitch of sound depends on intensity of sound which is independent of distance between source and detector.
View Solutionएक बुलेट ट्रैन 396 km/h की चाल से सीधी पटरी पर 1200 Hz की आवृति की ध्वनि उतपन्न करती हुई चल रही है । एक ध्वनि संसूचक स्रोत की गति रेखा से 1000 m की दूरी पर स्थित है । (a) जिस समय स्रोत संसूचक से न्यूनतम दूरी पर है, उस समय संसूचक द्वारा प्राप्त ध्वनि की आवृति निकाले । (b) जिस समय संसूचक 1200 Hz की आवृति की ध्वनि प्राप्त करता है, उस समय स्रोत एवं संसूचक के बीच की दूरी निकाले । हवा में ध्वनि की चाल 340 m/s ले ।
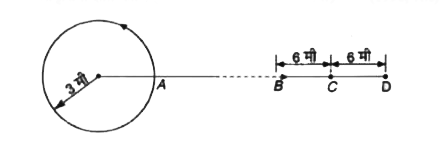
View Solutionएक ध्वनि - स्रोत 3 मी त्रिज्या की वृत्तीय कक्षा में 10 रेडियन से के कोणीय वेग से घूम रहा है। स्रोत से काफी दूर स्थित एक ध्वनि संसूचक BD रेखा के अनुदिश रेखीय सरल आवर्त गति कर रहा है जिसका आयाम BC = CD = 6 मी है।
संसूचक के दोलन की आवृत्ति 5/π प्रति सेकण्ड है। जब संसूचक बिन्दु B पर है , तब स्रोत बिन्दु A पर है। यदि स्रोत 340 हर्ट्ज आवृत्ति की अविरत ध्वनि तरंग उत्सर्जित करता है तो संसूचक द्वारा अभिलेखित उच्चतम व न्यूनतम आवृत्तियाँ ज्ञात कीजिए (ध्वनि की चाल = 340 मी / से)
View SolutionAn electric spark jumps along a straight line of length L = 10 m, emitting a pulse of sound that travels radially outward from the spark. (The spark is said to be a line source of sound.) The power of this acoustic emission is P=1.6×104 W. (a) What is the intensity I of the sound when it reaches a distance r = 12 m from the spark? (b) At what time rate PA is sound energy intercepted by an acoustic detector of area Ad=2.0cm2?, aimed at the spark and located a distance r = 12 m from the spark?
View SolutionA source emitting sound of frequency 180 Hz is placed in front of a wall at a distance of 2m from it. a detector is also placed in front of the wall at the same distance from it. The minimum distance between the source and the detector is x mtrs for which the detector shows a maxima of sound. Speed of sound in air = 360 m/s
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA source emitting sound of frequency 180 Hz is placed in front of a wall at a distance of 2m from it. a detector is also placed in front of the wall at the same distance from it. The minimum distance between the source and the detector is x mtrs for which the detector shows a maxima of sound. Speed of sound in air = 360 m/s
View SolutionA source of sound is moving along a circular orbit of radius 3m with an angular velocity of 10 red/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with amplitude BC = CD = 6m. The frequency of oscillation of the deterctor is (5/π) rev/sec. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340 Hz, find the maximum and the minimum frequencies recorded by the detector [velocity of sound =330 m/s].

View SolutionA line source of sound of length 10 m, emitting a pulse of sound that travels radially outward from the source. The power of the source is P = 1.0.x 104 W What is the approximated intensity I of the sound when it reaches a distance of 10 m from the source?
View SolutionL= 10m, लम्बाई का सरल रेखीय ध्वनि स्त्रोत ध्वनि का स्पंद उत्सर्जित करता है। जो स्रोत से त्रिज्य दि Prop में बाहर की ओर गतिमान है। स्त्रोत से 7m लम्बवत दूरी पर स्थित 1.2cm2 पष्ठ क्षेत्र के बेलनाकार ध्वनि संसूचक द्वारा प्राप्त ध्वनि उर्जा (mW में) क्या है। तरंगें संसूचक के पष्ठ पर लम्बवत पहुंचती है। स्त्रोत द्वारा उत्सर्जित ध्वनि के रूप में कुल शक्ति 2.2×104w है।
View Solution
