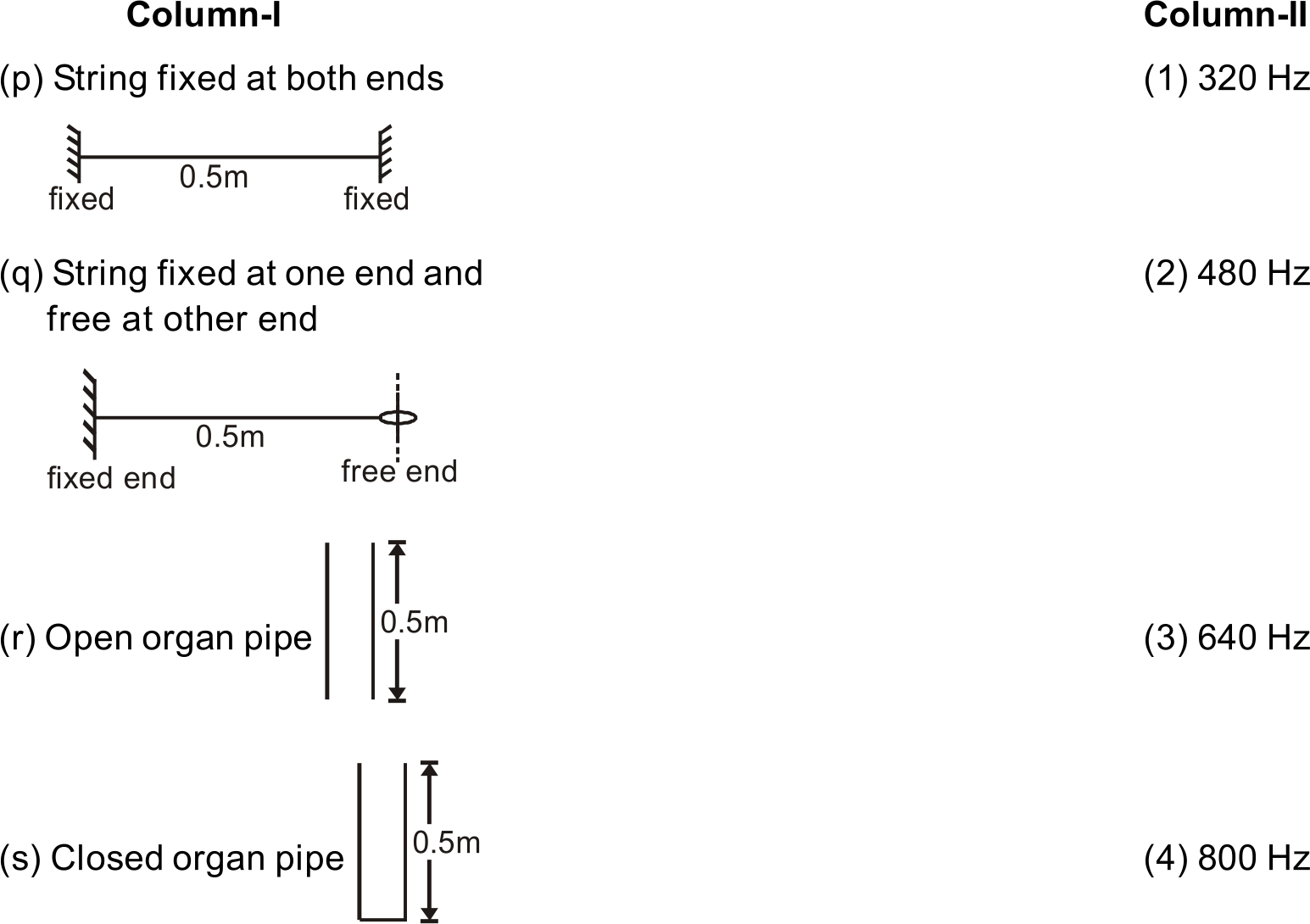
In each of the four situation of table -I a stretched string or an organ pipe is given with the required date. In case of string the tension in string is T = 102.4 N and the mass per unit length of string is 1 g/m . Speed of sound in air is 320 m/s. Neglect end corrections. Match each situation in table -I with the possible resonance frequencies given in Table -II.

$\begin{matrix} p & q & r & s (A) & 1 & 3 & 2 & 4 \end{matrix}$

$\begin{matrix} p & q & r & s (B) & 1 & 4 & 3 & 2 \end{matrix}$

$\begin{matrix} p & q & r & s (C) & 3 & 2 & 4 & 1 \end{matrix}$

$\begin{matrix} p & q & r & s (D) & 2 & 4 & 1 & 3 \end{matrix}$

Video Solution

Text Solution

Verified by Experts

(A) The fundamental frequency in the string.
$f_{0} = \frac{\sqrt{T / μ}}{2 l} = \sqrt{\frac{102.4}{1 \times 10^{- 3}}} \times \frac{1}{2 \times 0.5} H z = 320 H z$ .
Other possible resonance frequencies are $f_{A} and f_{0} = 320 H z, 640 H z, 960 H z$
(B)The fundamental frequency in the string.
$f_{0} = \frac{\sqrt{T / μ}}{4 l} = \frac{320}{4 \times 0.5} = 160 H z$ .
Other possible resonance frequencies are
$f_{B}$ =160 Hz, 480 Hz, 800 Hz.
(C )The fundamental frequency in both ends open organ pipe is
$f_{0} = \frac{v}{2 l} = \frac{320}{2 \times 0.5} = 320 H z$
Other possible resonance frequencies are
$f_{c} = 320 H z, 640 H z, 960 H z$
(D)The fundamental frequency in one end open organ pipe is
$f_{0} = \frac{v}{4 l} = \frac{320}{4 \times 0.5} = 160 H z$
Other possible resonance frequencies are $f_{D} = 160 H z, 480 H z, 800 H z$

Updated on:21/07/2023