An ideal gas consists of a large number of identical molecules. Absolute temperature of the gas is T(in kelvin). Molecular weight of gas is M and R is gas constant. Mathch the proper entries from column-2 to column-1 using the codes given below the columns. Column−1Column−II(P)Root mean square speed of molecules is greater than(1)√RTM(Q)Most probable speed of molecues is smaller than(2)1.5√RTM(R)Average velocity of a molecule is smaller than(3)2√RTM(S)Speed of a molecule may be greater than(4)2.5√RTM
pqrs2134
pqrs3142
pqrs1324
pqrs4231
To solve the problem, we need to match the statements in Column-1 with the correct entries in Column-2 based on the properties of an ideal gas.
1. Understanding Root Mean Square Speed (RMS Speed):
- The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
- This indicates that the RMS speed is proportional to the square root of the temperature (T) and inversely proportional to the square root of the molecular weight (M).
2. Most Probable Speed:
- The most probable speed (v_mp) of gas molecules is given by:
vmp=√2RTM
- This speed is always less than the RMS speed since √2<√3.
3. Average Speed:
- The average speed (v_avg) of gas molecules is given by:
vavg=√8RTπM
- This speed is also less than the RMS speed but greater than the most probable speed.
4. Speed of Molecules:
- The speed of individual molecules can vary widely, and thus it can be greater than any of the average speeds calculated above.
Matching Entries:
- (P): Root mean square speed of molecules is greater than √RTM.
- Match with (3) 2√RTM because vrms>vmp.
- (Q): Most probable speed of molecules is smaller than 1.5√RTM.
- Match with (2) 1.5√RTM because vmp<vrms.
- (R): Average velocity of a molecule is smaller than 2√RTM.
- Match with (1) √RTM because vavg<vmp<vrms.
- (S): Speed of a molecule may be greater than 2.5√RTM.
- Match with (4) 2.5√RTM since individual molecular speeds can exceed the calculated average speeds.
Final Matches:
- P → 3
- Q → 2
- R → 1
- S → 4
- The root mean square speed (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
- This indicates that the RMS speed is proportional to the square root of the temperature (T) and inversely proportional to the square root of the molecular weight (M).
- The most probable speed (v_mp) of gas molecules is given by:
vmp=√2RTM
- This speed is always less than the RMS speed since √2<√3.
- The average speed (v_avg) of gas molecules is given by:
vavg=√8RTπM
- This speed is also less than the RMS speed but greater than the most probable speed.
- The speed of individual molecules can vary widely, and thus it can be greater than any of the average speeds calculated above.
- Match with (3) 2√RTM because vrms>vmp.
- Match with (2) 1.5√RTM because vmp<vrms.
- Match with (1) √RTM because vavg<vmp<vrms.
- Match with (4) 2.5√RTM since individual molecular speeds can exceed the calculated average speeds.
- P → 3
- Q → 2
- R → 1
- S → 4
Topper's Solved these Questions
Similar Questions
In each situation of column-I,a process A→B→C is given for an ideal gas. Match the proper entries from column-2 to column-1 using the codes given below the columns
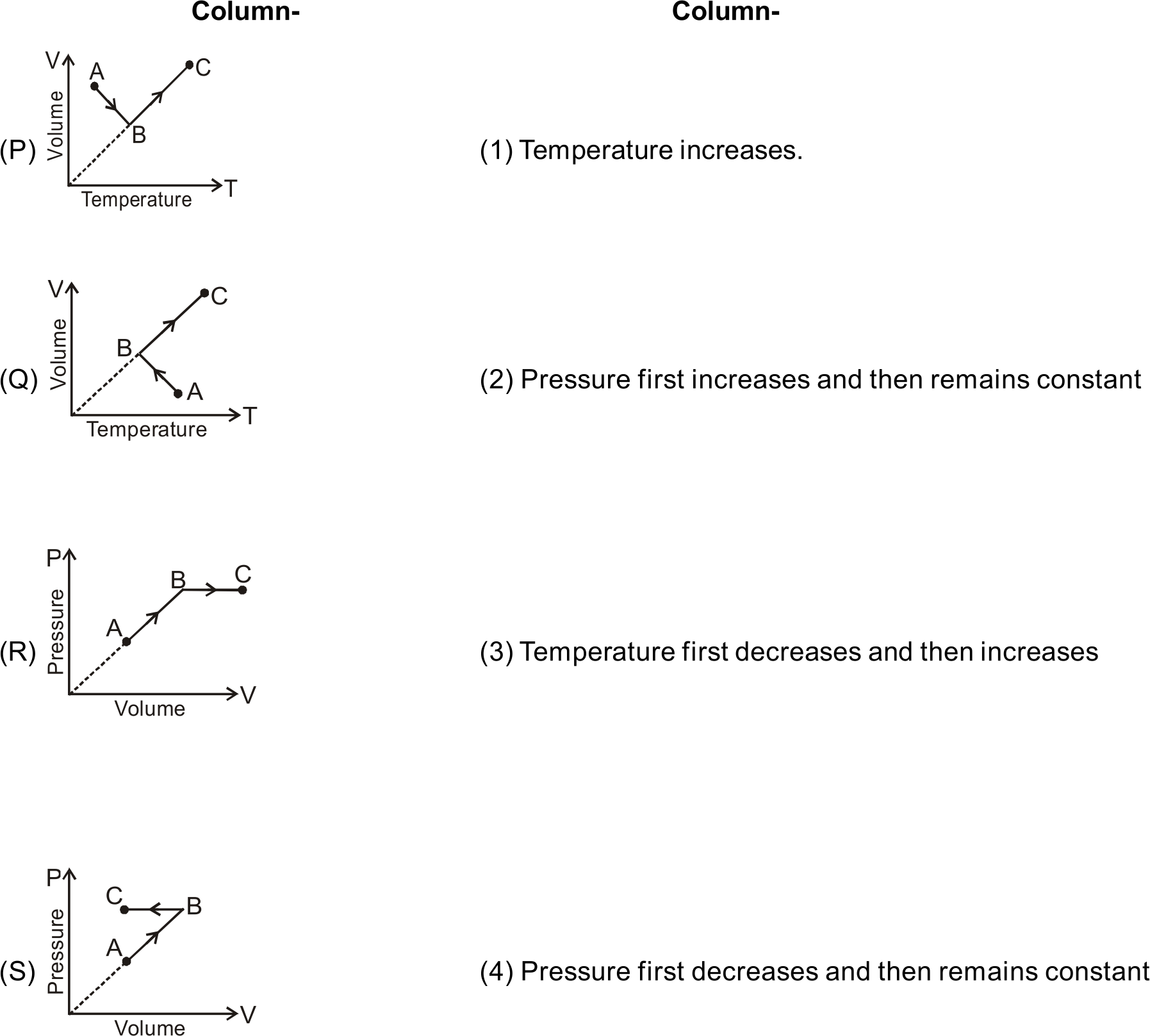
View SolutionIn column-II, some situations are given, and in column-I, their results are given. Mathc the proper entries from column-2 to column-1 using the codes iven below the columns

View SolutionFor a monotomic gas at temperature T, match the following columns.
ColumnIColumnII(A)Speed of sound(p)√2RT/M(B)RMS speed of gas molecules(q)√8RT/πM(C)Average speed of gas molecules(r)√3RT/M(D)Most probable speed of gas molecules(s)√5RT/3M
View SolutionThe absolute temperature of an ideal gas is….. to/than the average kinetic energy of the gas molecules.
View SolutionThe mean square speed of the molecules of a gas at absolute temperature T is proportional to
View SolutionThe absolute temperature of the gas is increased 3 times. What will be the increases in root mean square velocity of the gas molecules?
View SolutionThe most probable velocity of the molecules of a gas is 1 km/sec. The R.M.S velocity of the molecules is
View SolutionThe RMS velocity of the molecules of a gas is greater than the most probable velocity at the same temperature.
View SolutionThe average velocity of gas molecules is 400ms−1. Calculate their rms velocity at the same temperature.
View SolutionThe average velocity of molecules of a gas of molecular weight (M) at temperature (T) is
View Solution
