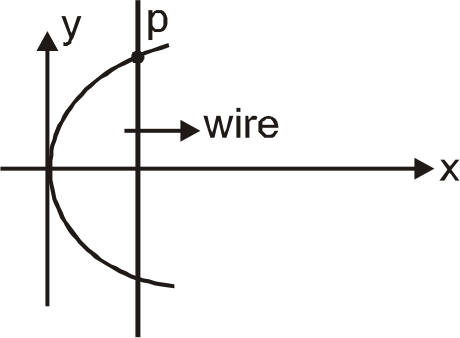
A wire is bent in a parabolic shape followed by equation x=4y2 consider origin as vertex of parabola a wire parallel toy axis moves with constant speed 4m/s along x-axis in the plane of bent wire. Then the acceleration of touching point of straight wire and parabolic wire is (when straight wire has x coordinates =4m)
12
14
2
4
x=4y2
dxdt=8ydydt
Vx=8yVy
Vx=4
ax=0 ltbr> 0=ax=8[y.ay+V2y]
−yay=V2y
∣∣ay∣∣=v2yy
∣∣ay∣∣=v2x64y3=1664×y3
at y=1⇒∣∣ay∣∣=14
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
02:53View SolutionWhen p−n junction diode is forward biased, then
05:47View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is
 02:26View Solution
02:26View SolutionA wire is bent in a parabolic shape followed by equation x=4y^(2) consider origin as vertex of parabola a wire parallel toy axis moves with constant speed 4m/s along x-axis in the plane of bent wire. Then the acceleration of touching point of straight wire and parabolic wire is (when straight wire has x coordinates =4m )
01:51View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
 01:32View Solution
01:32View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
04:07View SolutionIf a current I is flowing in a straight wire parallel to X - axis and magnetic field is in Y - axis then the wire experiences
05:03View SolutionIf the magnetic amplifier of a straight magnetic wire is M, what will be the magnetic amplifier of the wire if the wire is bent semicircularly?
02:44View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View Solutionकथन :- जब एक सीधे तार को L आकृति में मोडा जाता है तो इसका प्रतिरोध बढ़ जाता है।
कारण :- इलेक्ट्रॉन सीधे तार की अपेक्षा मुड़े हुए तार के अनुदिश गति करने में अधिक समय लेते हैं03:54View SolutionA piece of wire is bent in the shape of a parabola y = kx^2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
05:40View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
04:04View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
 04:16View Solution
04:16View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
03:10View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
05:42View Solution

