The temperature of isolated black body falls from $T_{1} to T_{2}$ in time t. Assuming Stefan’s law to hold, time t is proportional to :

A

$t \propto (\frac{1}{T_{2}} - \frac{1}{T_{1}})$

B

$t \propto (\frac{1}{T_{2}^{2}} - \frac{1}{T_{1}^{2}})$

C

$t \propto (\frac{1}{T_{2}^{3}} - \frac{1}{T_{1}^{3}})$

D

$t \propto (\frac{1}{T_{2}^{4}} - \frac{1}{T_{1}^{4}})$

Video Solution

Text Solution

Verified by Experts

Power radiated $P = 4 π r^{2} σ T^{4} = (m s \frac{d T}{d t})$
$- \int_{T_{1}}^{T_{2}} \frac{d T}{T^{4}} = c t \Rightarrow t = K [\frac{1}{T_{2}^{3}} - \frac{1}{T_{1}^{2}}]$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Assertion : Current versus potential difference (i-V) graph for a conductor at two different temperatures $T_{1}$ and $T_{2}$ is shown in figure. Hence $T_{1} > T_{2}$ .

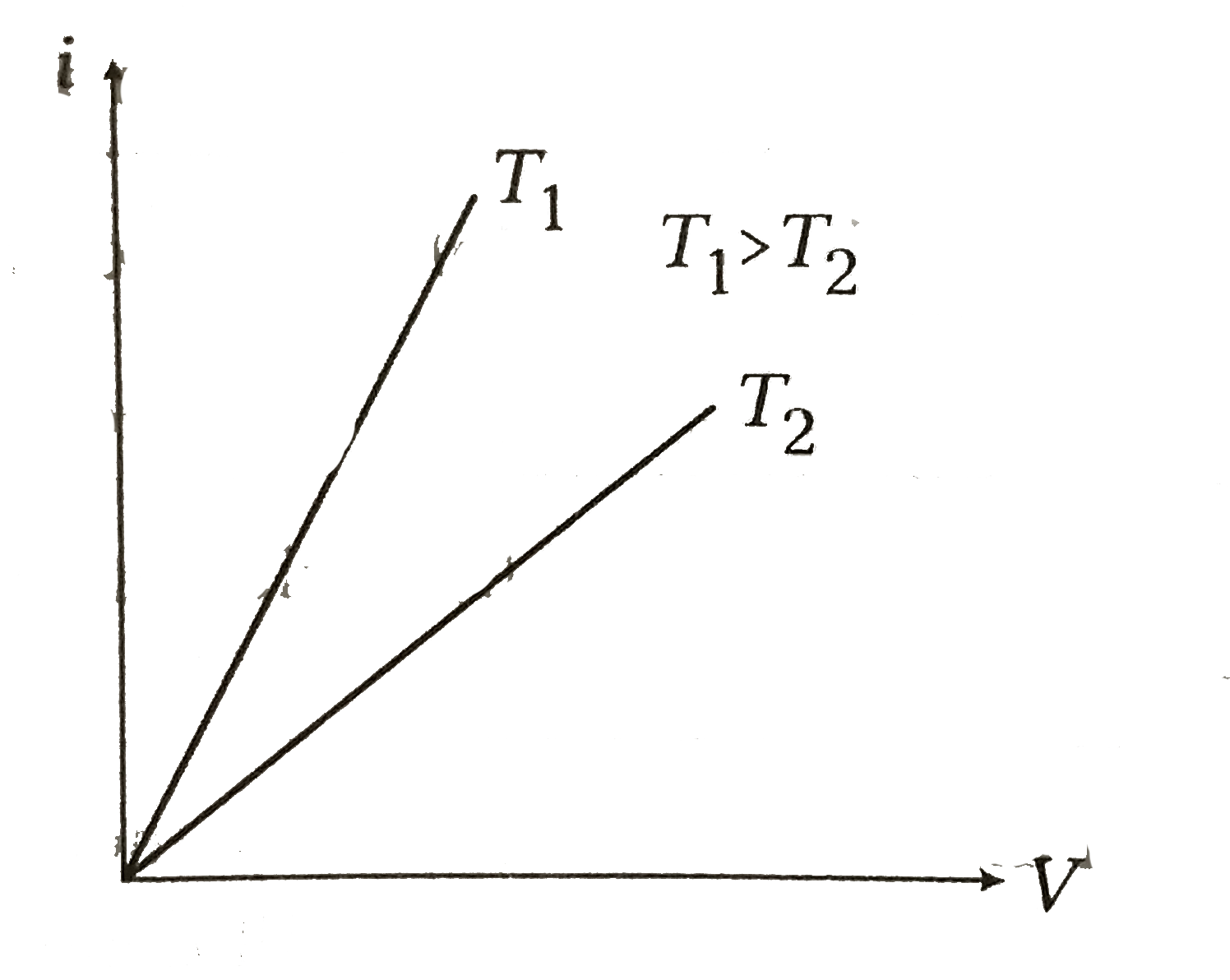
Reason : Resistance of a conductor increases with rise in temperature.
A $cos 2 θ$
B $sin 2 θ$
C $cot 2 θ$
D $tan 2 θ$

RESONANCE ENGLISH-REVISION DPP-All Questions

Home
Ask Doubt
Profile